A Variational Quantum Linear Solver Application to Discrete Finite-Element Methods
- PMID: 37190367
- PMCID: PMC10137608
- DOI: 10.3390/e25040580
A Variational Quantum Linear Solver Application to Discrete Finite-Element Methods
Abstract
Finite-element methods are industry standards for finding numerical solutions to partial differential equations. However, the application scale remains pivotal to the practical use of these methods, even for modern-day supercomputers. Large, multi-scale applications, for example, can be limited by their requirement of prohibitively large linear system solutions. It is therefore worthwhile to investigate whether near-term quantum algorithms have the potential for offering any kind of advantage over classical linear solvers. In this study, we investigate the recently proposed variational quantum linear solver (VQLS) for discrete solutions to partial differential equations. This method was found to scale polylogarithmically with the linear system size, and the method can be implemented using shallow quantum circuits on noisy intermediate-scale quantum (NISQ) computers. Herein, we utilize the hybrid VQLS to solve both the steady Poisson equation and the time-dependent heat and wave equations.
Keywords: Poisson equation; finite-element methods; heat equation; quantum algorithms; quantum computing; quantum variational algorithm.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

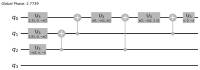
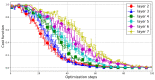




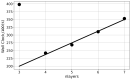


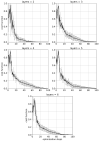



References
-
- Preskill J. Quantum computing and the entanglement frontier. [(accessed on 20 February 2023)];arXiv. 2012 Available online: http://arxiv.org/abs/1203.5813.1203.5813
-
- Arute F., Arya K., Babbush R., Bacon D., Bardin J.C., Barends R., Biswas R., Boixo S., Brandao F.G.S.L., Buell D.A., et al. Quantum supremacy using a programmable superconducting processor. [(accessed on 20 February 2023)];Nature. 2019 574:505–510. Available online: https://www.nature.com/articles/s41586-019-1666-5. - PubMed
-
- Connor E. The New Light-Based Quantum Computer Jiuzhang Has Achieved Quantum Supremacy. 2020. [(accessed on 20 February 2023)]. Available online: https://www.sciencenews.org/article/new-light-based-quantum-computer-jiu....
LinkOut - more resources
Full Text Sources

