Bayesian Data Selection
- PMID: 37206375
- PMCID: PMC10194814
Bayesian Data Selection
Abstract
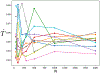
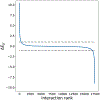
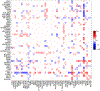
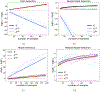
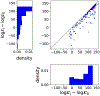
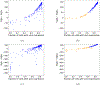
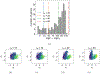
Insights into complex, high-dimensional data can be obtained by discovering features of the data that match or do not match a model of interest. To formalize this task, we introduce the "data selection" problem: finding a lower-dimensional statistic-such as a subset of variables-that is well fit by a given parametric model of interest. A fully Bayesian approach to data selection would be to parametrically model the value of the statistic, nonparametrically model the remaining "background" components of the data, and perform standard Bayesian model selection for the choice of statistic. However, fitting a nonparametric model to high-dimensional data tends to be highly inefficient, statistically and computationally. We propose a novel score for performing data selection, the "Stein volume criterion (SVC)", that does not require fitting a nonparametric model. The SVC takes the form of a generalized marginal likelihood with a kernelized Stein discrepancy in place of the Kullback-Leibler divergence. We prove that the SVC is consistent for data selection, and establish consistency and asymptotic normality of the corresponding generalized posterior on parameters. We apply the SVC to the analysis of single-cell RNA sequencing data sets using probabilistic principal components analysis and a spin glass model of gene regulation.
Keywords: Bayesian nonparametrics; Bayesian theory; Stein discrepancy; consistency; misspecification.
Figures


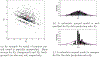



References
-
- Alon Uri. An Introduction to Systems Biology: Design Principles of Biological Circuits. CRC Press, July 2019.
-
- Anastasiou Andreas, Barp Alessandro, Briol François-Xavier, Ebner Bruno, Gaunt Robert E, Ghaderinezhad Fatemeh, Gorham Jackson, Gretton Arthur, Ley Christophe, Liu Qiang, Mackey Lester, Oates Chris J, Reinert Gesine, and Swan Yvik. Stein's method meets statistics: A review of some recent developments. arXiv preprint arXiv:2105.03481, May 2021.
-
- Banerjee Onureena, Ghaoui Laurent El, and d'Aspremont Alexandre. Model selection through sparse maximum likelihood estimation for multivariate Gaussian or binary data. Journal of Machine Learning Research, 9(Mar):485–516, 2008.
-
- Barp Alessandro, Briol Francois-Xavier, Duncan Andrew B, Girolami Mark, and Mackey Lester. Minimum Stein discrepancy estimators. arXiv preprint arXiv:1906.08283, June 2019.
-
- Barron Andrew R. Uniformly powerful goodness of fit tests. The Annals of Statistics, 17 (1):107–124, 1989.
Grants and funding
LinkOut - more resources
Full Text Sources
