Thermomagnetic properties and its effects on Fisher entropy with Schioberg plus Manning-Rosen potential (SPMRP) using Nikiforov-Uvarov functional analysis (NUFA) and supersymmetric quantum mechanics (SUSYQM) methods

Abstract

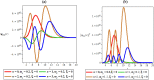
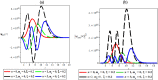
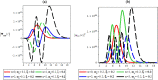
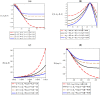
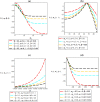
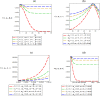
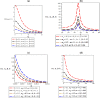
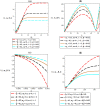
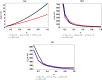
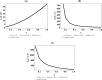
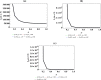
Thermomagnetic properties, and its effects on Fisher information entropy with Schioberg plus Manning-Rosen potential are studied using NUFA and SUSYQM methods in the presence of the Greene-Aldrich approximation scheme to the centrifugal term. The wave function obtained was used to study Fisher information both in position and momentum spaces for different quantum states by the gamma function and digamma polynomials. The energy equation obtained in a closed form was used to deduce numerical energy spectra, partition function, and other thermomagnetic properties. The results show that with an application of AB and magnetic fields, the numerical energy eigenvalues for different magnetic quantum spins decrease as the quantum state increases and completely removes the degeneracy of the energy spectra. Also, the numerical computation of Fisher information satisfies Fisher information inequality products, indicating that the particles are more localized in the presence of external fields than in their absence, and the trend shows complete localization of quantum mechanical particles in all quantum states. Our potential reduces to Schioberg and Manning-Rosen potentials as special cases. Our potential reduces to Schioberg and Manning-Rosen potentials as special cases. The energy equations obtained from the NUFA and SUSYQM were the same, demonstrating a high level of mathematical precision.

Figure 1

Variation of thermomagnetic energy spectra against the screening parameter in (a) the absence of AB and Magnetic field, (b) the presence of only magnetic field; (c) the presence of only AB field and (d) the presence of both magnetic and AB field.

Figure 2

(a) The variation of wave function plot against the radial distance in the absence of both AB and magnetic field. (b) The variation of probability density plot against the radial distance in absence of both AB and magnetic field.

Figure 3

(a) The variation of wave function plot against the radial distance in the presence of magnetic field. (b) The variation of probability density plot against the radial distance in the presence of magnetic field.

Figure 4

(a) The variation of wave function plot against the radial distance in the presence of AB field. (b) The variation of probability density plot against the radial distance in the presence of AB field.

Figure 5

(a) The variation of wave function plot against the radial distance in the presence of both magnetic and AB field. (b) The variation of probability density plot against the radial distance in the presence of both magnetic and AB field.

Figure 6

(a) Plot of partition function against magnetic flux $\left({\omega }_c\right)$ for different values of inverse temperature parameter $(\beta )$. (b) Plot of partition function against AB flux $\left(\xi \right)$ for different values of inverse temperature parameter ($\beta$). (c) Plot of partition function against inverse temperature parameter ($\beta$) for fixed value of ${\omega }_c$ and $\xi$ but for different values of maximum vibrational quantum number ($\lambda$). (d) Plot of partition function against the maximum vibrational quantum number ($\lambda$) for fixed value of ${\omega }_c$ and $\xi$ but for different values inverse temperature parameter ($\beta$).

Figure 7

(a) Plot of vibrational mean energy against magnetic flux $\left({\omega }_c\right)$ for different values of inverse temperature parameter $(\beta )$. (b) Plot of vibrational mean energy against AB flux $\left(\xi \right)$ for different values of inverse temperature parameter ($\beta$). (c) Plot of vibrational mean energy against inverse temperature parameter ($\beta$) for fixed value of ${\omega }_c$ and $\xi$ but for different values of maximum vibrational quantum number ($\lambda$). (d) Plot of vibrational mean energy against the maximum vibrational quantum number ($\lambda$) for fixed value of ${\omega }_c$ and $\xi$ but for different values inverse temperature parameter ($\beta$).

Figure 8

(a) Plot of vibrational heat capacity against magnetic flux $\left({\omega }_c\right)$ for different values of inverse temperature parameter $(\beta )$. (b) Plot of vibrational heat capacity against AB flux $\left(\xi \right)$ for different values of inverse temperature parameter ($\beta$). (c) Plot of vibrational heat capacity against inverse temperature parameter ($\beta$) for fixed value of ${\omega }_c$ and $\xi$ but for different values of maximum vibrational quantum number ($\lambda$). (d) Plot of vibrational heat capacity against the maximum vibrational quantum number ($\lambda$) for fixed value of ${\omega }_c$ and $\xi$ but for different values inverse temperature parameter ($\beta$).

Figure 9

(a) Plot of vibrational entropy against magnetic flux $\left({\omega }_c\right)$ for different values of inverse temperature parameter $(\beta )$. (b) Plot of vibrational entropy against AB flux $\left(\xi \right)$ for different values of inverse temperature parameter ($\beta$). (c) Plot of vibrational entropy against inverse temperature parameter ($\beta$) for fixed value of ${\omega }_c$ and $\xi$ but for different values of maximum vibrational quantum number ($\lambda$). (d) Plot of vibrational entropy against the maximum vibrational quantum number ($\lambda$), for fixed value of ${\omega }_c$ and $\xi$ but for different values inverse temperature parameter ($\beta$).

Figure 10

(a) Plot of vibrational Free energy against magnetic flux $\left({\omega }_c\right)$ for different values of inverse temperature parameter $(\beta )$. (b) Plot of vibrational Free energy against AB flux $\left(\xi \right)$ for different values of inverse temperature parameter ($\beta$). (c) Plot of vibrational Free energy against inverse temperature parameter ($\beta$) for fixed value of ${\omega }_c$ and $\xi$ but for different values of maximum vibrational quantum number ($\lambda$). (d) Plot of vibrational Free energy against the maximum vibrational quantum number ($\lambda$) for fixed value of ${\omega }_c$ and $\xi$ but for different values inverse temperature parameter ($\beta$).

Figure 11

(a) Plot of magnetization against magnetic flux $\left({\omega }_c\right)$ for different values of inverse temperature parameter $(\beta )$. (b) Plot of magnetization against AB flux $\left(\xi \right)$ for different values of inverse temperature parameter ($\beta$). (c) Plot of magnetization against inverse temperature parameter ($\beta$) for fixed value of ${\omega }_c$ and $\xi$ but for different values of maximum vibrational quantum number ($\lambda$). (d) Plot of magnetization against the maximum vibrational quantum number ($\lambda$) for fixed value of ${\omega }_c$ and $\xi$ but for different values inverse temperature parameter ($\beta$).

Figure 12

(a) Plot of magnetic susceptibility against magnetic flux $\left({\omega }_c\right)$ for different values of inverse temperature parameter $(\beta )$. (b) Plot of magnetic susceptibility against AB flux $\left(\xi \right)$ for different values of inverse temperature parameter ($\beta$). (c) Plot of magnetic susceptibility against inverse temperature parameter ($\beta$) for fixed value of ${\omega }_c$ and $\xi$ but for different values of maximum vibrational quantum number ($\lambda$). (d) Plot of magnetic susceptibility against the maximum vibrational quantum number ($\lambda$) for fixed value of ${\omega }_c$ and $\xi$ but for different values inverse temperature parameter ($\beta$).

Figure 13

(a) Plot of persistent current against magnetic flux $\left({\omega }_c\right)$ for different values of inverse temperature parameter $(\beta )$. (b) Plot of persistent current against AB flux $\left(\xi \right)$ for different values of inverse temperature parameter ($\beta$). (c) Plot of persistent current against inverse temperature parameter ($\beta$) for fixed value of ${\omega }_c$ and $\xi$ but for different values of maximum vibrational quantum number ($\lambda$). (d) Plot of persistent current against the maximum vibrational quantum number ($\lambda$) for fixed value of ${\omega }_c$ and $\xi$ but for different values inverse temperature parameter ($\beta$).

Figure 14

(a) The plot of position space Fisher entropy against the screening parameter for $n=0$. (b) The plot of momentum space Fisher entropy against the screening parameter for $n=0$. (c) The plot of product of position and momentum space Fisher entropy against the screening parameter for $n=0$.

Figure 15

(a) The plot of position space Fisher entropy against the screening parameter for $n=1$ . (b) The plot of momentum space Fisher entropy against the screening parameter for $n=1$. (c) The plot of product of position and momentum space Fisher entropy against the screening parameter for $n=1$.

Figure 16

(a) The plot of position space Fisher entropy against the screening parameter for $n=2$. (b) The plot of momentum space Fisher entropy against the screening parameter for $n=2$. (c) The plot of product of position and momentum space Fisher entropy against the screening parameter for $n=2$.

Figure 17

(a) The plot of position space Fisher entropy against the screening parameter for $n=3$. (b) The plot of momentum space Fisher entropy against the screening parameter for $n=3$. (c) The plot of product of position and momentum space Fisher entropy against the screening parameter for $n=3$.