Factorization and pseudofactorization of weighted graphs
- PMID: 37213330
- PMCID: PMC10194401
- DOI: 10.1016/j.dam.2023.04.019
Factorization and pseudofactorization of weighted graphs
Abstract
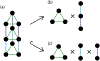
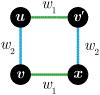
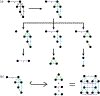
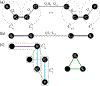
For unweighted graphs, finding isometric embeddings of a graph is closely related to decompositions of into Cartesian products of smaller graphs. When is isomorphic to a Cartesian graph product, we call the factors of this product a factorization of . When is isomorphic to an isometric subgraph of a Cartesian graph product, we call those factors a pseudofactorization of . Prior work has shown that an unweighted graph's pseudofactorization can be used to generate a canonical isometric embedding into a product of the smallest possible pseudofactors. However, for arbitrary weighted graphs, which represent a richer variety of metric spaces, methods for finding isometric embeddings or determining their existence remain elusive, and indeed pseudofactorization and factorization have not previously been extended to this context. In this work, we address the problem of finding the factorization and pseudofactorization of a weighted graph , where satisfies the property that every edge constitutes a shortest path between its endpoints. We term such graphs minimal graphs, noting that every graph can be made minimal by removing edges not affecting its path metric. We generalize pseudofactorization and factorization to minimal graphs and develop new proof techniques that extend the previously proposed algorithms due to Graham and Winkler [Graham and Winkler, '85] and Feder [Feder, '92] for pseudofactorization and factorization of unweighted graphs. We show that any -vertex, -edge graph with positive integer edge weights can be factored in time, plus the time to find all pairs shortest paths (APSP) distances in a weighted graph, resulting in an overall running time of time. We also show that a pseudofactorization for such a graph can be computed in time, plus the time to solve APSP, resulting in an running time.
Conflict of interest statement
Declarations of Interest The authors declare that they have no competing interests.
Figures

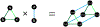
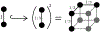

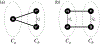
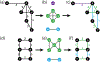
References
-
- Baum Eric B. Building an associative memory vastly larger than the brain. Science, 268(5210):583–585, 1995. - PubMed
-
- Cherry Kevin M and Qian Lulu. Scaling up molecular pattern recognition with DNA-based winner-take-all neural networks. Nature, 559(7714):370–376, 2018. - PubMed
-
- Deza Michel and Laurent Monique. Additional notes. In Graham RL, Korte B, Lovasz Bonn L., Wigderson A, and Ziegler GM, editors, Geometry of Cuts and Metrics, chapter 20.4, pages 308–311. Springer, 1997.
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
