Effective dose window for containing tumor burden under tolerable level

Abstract

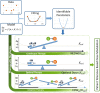
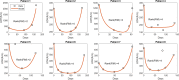
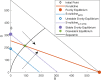
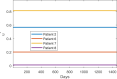
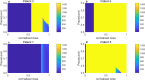
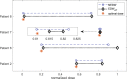
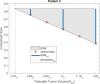
A maximum-tolerated dose (MTD) reduces the drug-sensitive cell population, though it may result in the competitive release of drug resistance. Alternative treatment strategies such as adaptive therapy (AT) or dose modulation aim to impose competitive stress on drug-resistant cell populations by maintaining a sufficient number of drug-sensitive cells. However, given the heterogeneous treatment response and tolerable tumor burden level of individual patients, determining an effective dose that can fine-tune competitive stress remains challenging. This study presents a mathematical model-driven approach that determines the plausible existence of an effective dose window (EDW) as a range of doses that conserve sufficient sensitive cells while maintaining the tumor volume below a threshold tolerable tumor volume (TTV). We use a mathematical model that explains intratumor cell competition. Analyzing the model, we derive an EDW determined by TTV and the competitive strength. By applying a fixed endpoint optimal control model, we determine the minimal dose to contain cancer at a TTV. As a proof of concept, we study the existence of EDW for a small cohort of melanoma patients by fitting the model to longitudinal tumor response data. We performed identifiability analysis, and for the patients with uniquely identifiable parameters, we deduced patient-specific EDW and minimal dose. The tumor volume for a patient could be theoretically contained at the TTV either using continuous dose or AT strategy with doses belonging to EDW. Further, we conclude that the lower bound of the EDW approximates the minimum effective dose (MED) for containing tumor volume at the TTV.

Fig. 1. Workflow: development of a mathematical model, integration with data by fitting the model to data, identifiability analysis on the estimated parameters.

Dynamical analysis of the model and the parameter estimates provide a ground for modulating dose depending on the patient-specific TTV (K_tol). Three different treatment strategies: continuous therapy with a dose belongs to EDW (defined in equation (4)), optimal dose continuous therapy (defined in equation (19)), and adaptive therapy (defined in equation (20)). S: drug-sensitive cell population (the green circle), R: drug-resistant cell population (the orange circle), negative control line between S and R indicates competitive stress on R by S. The vertical gray axis labeled S + R represents the tumor volume, while the horizontal axis shows the time. Solid black on the horizontal axis resembles treatment-on and the thin blue part resembles treatment-off. The orange horizontal solid line represents the TTV(K_tol) and the dashed line shows the growth of the tumor volume. Continuous therapy represses the competition due to the continuous reduction of the S cell population and ends up with a volume below the TTV(K_tol). The optimal therapy applies a dose that balances the competitive stress, the drug, and TTV(K_tol). Adaptive therapy utilizes treatment on and off which tilts the seesaw on each side between the drug and S to R inhibition during treatment on and off.

Fig. 2. Model dynamics.

The upper panel (a) shows the bifurcation diagram. K_tol is the tolerable tumor volume (TTV), which is also assumed to be the threshold tumor burden that determines tumor progression. The vertical gray dotted lines divide the domain into three parts, showing the equilibria for Cases I, II, and III. The solid orange line shows the stable R-only equilibrium and the solid blue line shows the stable S-only equilibrium. The dashed blue line indicates an unstable S-only equilibrium. The dash-dot blue and orange lines indicate the S-cell and R-cell populations, respectively, in the unstable coexistence equilibrium. The solid black line represents the tolerable tumor volume and corresponding drug-induced death rate. The horizontal double arrow indicates the EDW. The lower panel shows the phase diagrams for cases III (b), II (c), and I (d) (from left to right). Triangular regions indicate the phase space. The dotted blue and orange lines represent the S- and R- nullclines, respectively. The dashed lines with different shades of gray are the trajectories starting from different points in the phase space where empty dots indicate initial conditions. The solid black curve (b) shows the separatrix in case III. The orange-filled dots show the stable R-only equilibrium in all the cases. The blue-filled dot in Case III indicates a stable S-only equilibrium. The blue empty dot shows the unstable S-only equilibrium in Case II. It is observed that the trajectories starting from the same three points (gray empty dots) evolve in a different manner as δ changes. The assumed parameter values for the above diagram are r = 0.02, c = 3, K = 1000, and K_tol = 500, and the initial conditions for the phase portraits are (S(0), R(0)) = (800, 190), (200, 200), and (450, 500).

Fig. 3. Fitting with biomarker (LDH) data.

The circles indicate the data points for each patient and the solid line shows the model-predicted dynamics of the LDH level in international units per liter (IU/L). FIM: Fisher information matrix. It should be noted that the second and fourth data points in the case of Patients five and eight, respectively, were excluded while fitting, as these two instances resemble deviations from the regular trend observed through the other data points, which could be a consequence of other physical problems. Owing to the lack of detail in the patient’s history, we proceed with this assumption.

Fig. 4. Dose modulates the basin of attraction.

The triangular region shows the phase space for patient 2. The initial cell composition is shown by the gray diamond (◇). The solid orange line shows the R-nullcline (equation (3)), which is invariant to δ, and the solid orange circle represents the R-only equilibrium. The dotted blue line shows the S-nullcline (equation (2)) with the MTD, and the empty blue circle is the unstable S-only equilibrium. The dotted purple line shows the S-nullcline (equation (2)) with 70% of the MTD (belonging to the EDW (equation (4))), and the filled purple circle is the stable S-only equilibrium. The solid black line indicates the separatrix. The two arrows indicate the direction in which the separatrix and S-nullcline are shifted when δ decreases.

Fig. 5. Time dependent dose and corresponding tumor evolution for patients 2.

a The surface plot shows the time-dependent optimal (OT) dose for a range of values of B for Patient 2. b The blue and black lines show the change in the total cancer volume with OT (contained at the initial volume) and with MTD, respectively. c The blue and black lines show the change in the number of R-cells with OT (contained at the initial volume) and with MTD, respectively.

Fig. 6. Time-dependent optimal dose for the patients 2, 6, 7, and 8.

u^*(t) = 1 corresponds to the MTD. Therefore, in all patients, we observed that a time-dependent dose smaller than the MTD is recommended for optimal therapy.

Fig. 7. The pause level does not affect the TTP for a window of doses.

The TTP in days under AT with different pause levels and normalized doses for patient (a) 2, (b) 6, (c) 7, and (d) 8. The color bar indicates TTP in days.

Fig. 8. Effective dose window (EDW) and minimum effective dose (MED).

The blue dashed line and black dotted lines resemble the NEDW and EDW_AT. The orange asterisk (*) indicates the optimal dose, designated as the MED. The dose windows for patient seven are very narrow, which is magnified in the inset.

Fig. 9. Doses adjusted to tolerable tumor burden.

Effective dose window (the shaded gray region) is bounded by the upper horizontal (determined by the competition coefficient) and the lower inclined black line (the minimum effective dose). The vertical blue lines show the effective dose window for adaptive therapy for different TTV adopted from Supplementary Fig. 5. The orange asterisk indicates an optimal dose, which coincides with the lower bound of the effective dose window. The vertical dashed line resembles the threshold value of K_tol below which the tumor cannot be contained.