A leader cell triggers end of lag phase in populations of Pseudomonas fluorescens
- PMID: 37223352
- PMCID: PMC10117806
- DOI: 10.1093/femsml/uqac022
A leader cell triggers end of lag phase in populations of Pseudomonas fluorescens
Erratum in
-
Correction to: A leader cell triggers end of lag phase in populations of Pseudomonas fluorescens.Microlife. 2023 Oct 20;4:uqad040. doi: 10.1093/femsml/uqad040. eCollection 2023. Microlife. 2023. PMID: 37869483 Free PMC article.
Abstract
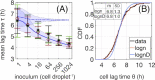
The relationship between the number of cells colonizing a new environment and time for resumption of growth is a subject of long-standing interest. In microbiology this is known as the "inoculum effect." Its mechanistic basis is unclear with possible explanations ranging from the independent actions of individual cells, to collective actions of populations of cells. Here, we use a millifluidic droplet device in which the growth dynamics of hundreds of populations founded by controlled numbers of Pseudomonas fluorescens cells, ranging from a single cell, to one thousand cells, were followed in real time. Our data show that lag phase decreases with inoculum size. The decrease of average lag time and its variance across droplets, as well as lag time distribution shapes, follow predictions of extreme value theory, where the inoculum lag time is determined by the minimum value sampled from the single-cell distribution. Our experimental results show that exit from lag phase depends on strong interactions among cells, consistent with a "leader cell" triggering end of lag phase for the entire population.
Keywords: collective behavior; extreme value theory; growth dynamics; high-throughput millifluidics; microbial population biology.
© The Author(s) 2022. Published by Oxford University Press on behalf of FEMS.
Conflict of interest statement
No competing interests are declared.
Figures



Comment in
-
Correction to: A leader cell triggers end of lag phase in populations of Pseudomonas fluorescens.Microlife. 2023 Oct 20;4:uqad040. doi: 10.1093/femsml/uqad040. eCollection 2023. Microlife. 2023. PMID: 37869483 Free PMC article.
Similar articles
-
Correlation between the change in the kinetics of the ribosomal RNA rrnB P2 promoter and the transition from lag to exponential phase with Pseudomonas fluorescens.Int J Food Microbiol. 2008 Jan 15;121(1):11-7. doi: 10.1016/j.ijfoodmicro.2007.10.003. Epub 2007 Nov 1. Int J Food Microbiol. 2008. PMID: 18036694
-
Correction to: A leader cell triggers end of lag phase in populations of Pseudomonas fluorescens.Microlife. 2023 Oct 20;4:uqad040. doi: 10.1093/femsml/uqad040. eCollection 2023. Microlife. 2023. PMID: 37869483 Free PMC article.
-
Effect of starvation on expression of the ribosomal RNA rrnB P2 promoter during the lag phase of Pseudomonas fluorescens.Int J Food Microbiol. 2007 Mar 20;114(3):307-15. doi: 10.1016/j.ijfoodmicro.2006.09.022. Epub 2006 Dec 13. Int J Food Microbiol. 2007. PMID: 17169452
-
Cell division theory and individual-based modeling of microbial lag: part I. The theory of cell division.Int J Food Microbiol. 2005 Jun 15;101(3):303-18. doi: 10.1016/j.ijfoodmicro.2004.11.016. Int J Food Microbiol. 2005. PMID: 15925713 Review.
-
On the duration of the microbial lag phase.Curr Genet. 2019 Jun;65(3):721-727. doi: 10.1007/s00294-019-00938-2. Epub 2019 Jan 21. Curr Genet. 2019. PMID: 30666394 Free PMC article. Review.
Cited by
-
Measuring and modeling the dynamics of mitotic error correction.Proc Natl Acad Sci U S A. 2024 Jun 18;121(25):e2323009121. doi: 10.1073/pnas.2323009121. Epub 2024 Jun 14. Proc Natl Acad Sci U S A. 2024. PMID: 38875144 Free PMC article.
-
Impact of micro-habitat fragmentation on microbial population growth dynamics.ISME J. 2025 Jan 2;19(1):wrae256. doi: 10.1093/ismejo/wrae256. ISME J. 2025. PMID: 39711055 Free PMC article.
-
Toxicological and Functional Assessment of Minicell-Encapsulated dsRNA on Biocontrol Agents in Agriculture.ACS Environ Au. 2025 Jun 17;5(4):427-441. doi: 10.1021/acsenvironau.5c00067. eCollection 2025 Jul 16. ACS Environ Au. 2025. PMID: 40687506 Free PMC article.
-
Fragmented micro-growth habitats present opportunities for alternative competitive outcomes.Nat Commun. 2024 Aug 31;15(1):7591. doi: 10.1038/s41467-024-51944-z. Nat Commun. 2024. PMID: 39217178 Free PMC article.
References
-
- Baraban L, Bertholle F, Salverda MLMet al. . Millifluidic droplet analyser for microbiology. Lab Chip. 2011;11:4057–62. - PubMed
LinkOut - more resources
Full Text Sources
