Thermal transport in kinked nanowires through simulation

Abstract

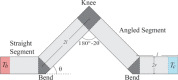
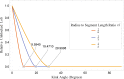
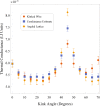
The thermal conductance of nanowires is an oft-explored quantity, but its dependence on the nanowire shape is not completely understood. The behaviour of the conductance is examined as kinks of varying angular intensity are included into nanowires. The effects on thermal transport are evaluated through molecular dynamics simulations, phonon Monte Carlo simulations and classical solutions of the Fourier equation. A detailed look is taken at the nature of heat flux within said systems. The effects of the kink angle are found to be complex, influenced by multiple factors including crystal orientation, details of transport modelling, and the ratio of mean free path to characteristic system lengths. The effect of varying phonon reflection specularity on the heat flux is also examined. It is found that, in general, the flow of heat through systems simulated through phonon Monte Carlo methods is concentrated into a channel smaller than the wire dimensions, while this is not the case in the classical solutions of the Fourier model.

Keywords: ballistic transport; kinked nanowire; molecular dynamics; phonon Monte Carlo; thermal transport.

Figure 1

Schematic of kinked wire with nomenclature. The use of the length 2l is a typical example. Note the relation between the angle at the bend (θ) and the angle at the knee (180° − 2θ).

Figure 2

Top: thermal conductance of kinked nanowires with varying base segment length. Bottom: thermal conductance of MD-simulated nanowires for varying kink angles. Radii of wires varied from 5 to 15 lattice constants. Error bars are 1 standard error. The purple dashed line indicates the thermal conductance of a straight nanowire with similar length, a radius of 10 lattice constants, and the lattice orientation along the [110] direction. The shaded purple area indicates 1 standard error from the dashed line. Right: 2D reference sketches for a system with various bend kink angles with r/l = 1/3 and two lengths of l in each angled segment. This roughly corresponds to the blue squares data set.

Figure 3

Relative LoS through kinked wires as a function of both kink angle and radius to segment length ratio. Values are expressed as a ratio of total LoS area to maximum theoretical, and threshold angles where LoS = 0 are highlighted.

Figure 4

Comparison of thermal conductances for kinked wires, straight wires with angled lattices, and a series resistance estimate.

Figure 5

Thermal conductances calculated from 2D PMC simulations of kinked nanowires with varying kink angles. Three scattering rates are shown. The purple line shows the (rescaled) conductance yielded by the Fourier result.

Figure 6

2D vector plots of heat flux in 45° kinked wires. The colour mapping indicates the value of the heat flux, normalized by the mean flux, through the system, yielding a unitless flux. Top: Fourier steady-state calculation. Middle: PMC simulation. Bottom: PMC with 10× multiplier on the scattering rate.

Figure 7

Colour maps of heat flux for PMC simulation (left column) and Fourier equation solution (right column) in kinked wires with kink angles of 15°, 30°, 45°, and 60°. The colour mapping indicates the value of the heat flux, normalized by the mean flux, through the system. The flux is unitless.

Figure 8

Clipped colour maps of normalized heat flux for the 45° system using (from top to bottom) PMC, PMC with 5× scattering, PMC with 10× scattering, and Fourier solution. The colour bar shows values where the colour scale is applied and where it is set to grey to improve resolution.

Figure 9

Clipped colour maps of normalized heat flux for 45° systems using (from top to bottom) PMC with 0% specularity, PMC with 50% specularity, PMC with 100% specularity and Fourier solution. The colour scale shows values where colour is clipped (set to grey) to improve resolution.

Figure 10

Image of the MD system for a wire with a kink angle of 40°. Visualization via OVITO [48].