The effect of the subthreshold oscillation induced by the neurons' resonance upon the electrical stimulation-dependent instability

Abstract

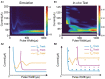
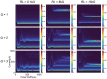
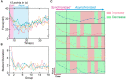
Repetitive electrical nerve stimulation can induce a long-lasting perturbation of the axon's membrane potential, resulting in unstable stimulus-response relationships. Despite being observed in electrophysiology, the precise mechanism underlying electrical stimulation-dependent (ES-dependent) instability is still an open question. This study proposes a model to reveal a facet of this problem: how threshold fluctuation affects electrical nerve stimulations. This study proposes a new method based on a Circuit-Probability theory (C-P theory) to reveal the interlinkages between the subthreshold oscillation induced by neurons' resonance and ES-dependent instability of neural response. Supported by in-vivo studies, this new model predicts several key characteristics of ES-dependent instability and proposes a stimulation method to minimize the instability. This model provides a powerful tool to improve our understanding of the interaction between the external electric field and the complexity of the biophysical characteristics of axons.

Keywords: Circuit-Probability theory; neural modeling; neural oscillation; subthreshold oscillation; threshold fluctuation.

Figure 1

The testing setup, stimulation protocol and the result sample. (A) The testing setup for measuring the force generated by sciatic nerve stimulations; (B) The fabricated flexible neural probe used for sciatic nerve stimulations; (C) The electrode pads on the neural probe for stimulations; (D) The flexible neural probe implanted to the sciatic nerve; (E1) The stimulation protocol. Each stimulation train contains 5 current pulses with 16.7 ms as latency. The latency between each train is 1 s. (E2) The sample of measured force showing non-monotonous fluctuation. f₁~f₃₀ are the force pulses generated by the 30 pulse tains in (E1). (E3) A sample of the instability curve of the measured force, defined as ${\xi }_e=\frac{F_{std}}{F_{mean}}$, by changing the current amplitudes.

Figure 2

The concept of the C-P theory and the definition of instability in modeling. (A) The neural response of electrical stimulations: a suprathreshold stimulation will generate an action potential, while a subthreshold stimulation will induce a subthreshold oscillation. (B) The equivalent circuit with an RLC configuration to model the neurons. (C) The resultant voltage waveform across the C_Membrane was recorded when a positive-first biphasic square waveform current of varying amplitudes and pulse widths was applied. (D) The concept of C-P theory. The subthreshold oscillation can be duplicated by the voltage response of the RLC circuit in (B). The part of the voltage exceeding the threshold will be involved in the calculation of the probability of generating an action potential. (E) Probability calculation of different current amplitudes by changing pulse widths (probability mapping). (F) Measured force curves of different current amplitudes by changing pulse widths in in-vivo testing. (G) The definition of ES-dependent instability: assuming that the threshold will have a fluctuation in the range of ±, the instability in modeling is defined as ${\xi }_s=\frac{P_{Thr+}-P_{Thr-}}{P_{Thr}}$.

Figure 3

The illustrative explanation of the instability peaks in modeling. (A) Modeling results show several instability peaks in the instability curve by the definition of ${\xi }_s=\frac{P_{Thr+▵}-P_{Thr-▵}}{P_{Thr}}$; (B) The voltage oscillation shows several oscillation peaks corresponding to the instability peaks in (A); (C) Illustrative explanation about how the voltage oscillation peaks induce instability peaks; (D) The modeling of instability peaks by the definition of ${\xi }_s=\frac{P^{\prime }(I)}{P(I)}$.

Figure 4

The patterns of the instability peaks in in-vivo tests are reproduced by modeling. (A1–A3) The heat map of the instability by changing both pulse width and current amplitude; (B1–B3) The captured profile of the instability curve at a specific pulse width; (C1–C3) The measured instability curves to be reproduced by (B1–B3).

Figure 5

The moving tacks of instability peaks in in-vivo test are reproduced by modeling. (A1) The heat map of the instability by modeling; (A2) The tracks of the three instability peaks in (A1); (B1) The measured heat map of the instability by in-vivo test; (B2) The recognized positions and tracks of the instability peaks in (B1).

Figure 6

A parameter comparison by modeling. The resistor connected in series with the inductor and the quality factor of the circuit are selected as the variables.

Figure 7

The methods to improve the ES-dependent stability by selecting proper stimuli parameters. (A) An overlapping of the contour map and its instability mapping. The horizontal yellow line is the parameter path with the minimal mean instability in all horizontal lines; the vertical purple line is the parameter path with the minimum mean instability in all vertical lines. (B) The calculated mean instability of all horizontal lines (yellow) and vertical lines (purple). (C) The same overlapping map as (A) with green region (low instability) and red region (high instability). (D) A case demonstration of the instability calculation of the 70% contour line by setting current (upper) and pulse width (lower) as x-axis. The curve higher than ξ_Threshold is labeled in red, while the curve lower than ξ_Threshold is labeled in green.

Figure 8

A comparison of the modeling by using an RC circuit. (A) The RC circuit used in modeling; (B) A representative voltage waveform (blue line) by applying a square current (red dash line). Only the voltage (filled with orange color) exceeding the threshold (green line) is calculated in probability calculus. (C) The probability is calculated by changing the current amplitude; (D1–D3) The heat map of the instability by changing the value of the capacitance.

Figure 9

A comparison between square and sine current waveform. (A) The measured force; (B) The calculated instability curve; (C) Re-processed instability curves by setting the force as x-axis.

Figure 10

The modeling and in-vivo results show the trade-off between ES-dependent stability and linearity. (A1) A representative probability curve of modeling showing several abrupt change points; (A2) The calculated instability curve shows the positions of the peaks corresponding to the positions of the abrupt change points; (B1) A presentative force curve of the in-vivo test showing several abrupt change points; (B2) The instability curve shows the positions of the peaks corresponding to the positions of the abrupt change points. (C1–C3) The force-current curve with error bar (blue) and the instability-current curve (orange) shows other results of square wave tests on the sciatic nerve.

Figure 11

The illustrative explanation of the historical path divergence issue.

Figure 12

The testing data to validate the historical path divergence issue. (A) The five measured force curves with the same testing parameters, and the synchroized and asynchronized area in (C); (B) The standard deviation of the force curve in (A). Every five points in (A) are calculated as one data point in (B); (C) The first fifteen points of the five curves in (A) are compared. The changing trends are labeled in colors (red refers to increasing, and green refers to decreasing).