Shape complexity in cluster analysis

Abstract

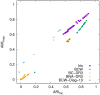
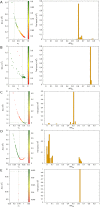
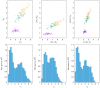
In cluster analysis, a common first step is to scale the data aiming to better partition them into clusters. Even though many different techniques have throughout many years been introduced to this end, it is probably fair to say that the workhorse in this preprocessing phase has been to divide the data by the standard deviation along each dimension. Like division by the standard deviation, the great majority of scaling techniques can be said to have roots in some sort of statistical take on the data. Here we explore the use of multidimensional shapes of data, aiming to obtain scaling factors for use prior to clustering by some method, like k-means, that makes explicit use of distances between samples. We borrow from the field of cosmology and related areas the recently introduced notion of shape complexity, which in the variant we use is a relatively simple, data-dependent nonlinear function that we show can be used to help with the determination of appropriate scaling factors. Focusing on what might be called "midrange" distances, we formulate a constrained nonlinear programming problem and use it to produce candidate scaling-factor sets that can be sifted on the basis of further considerations of the data, say via expert knowledge. We give results on some iconic data sets, highlighting the strengths and potential weaknesses of the new approach. These results are generally positive across all the data sets used.

Fig 1. ARI_fnc versus AMI_max for all partitions resulting from scaling as in the rightmost column of Table 2.

Fig 2

Results of the random trials with Problem P on Iris (A), BCW (B), BC-DR3 (C), BNA-DR3 (D), and BCW-Diag-10 (E), expanding on the summary given on the rightmost column of Table 2. Each point on each left panel corresponds to a trial and is color-coded according to the accompanying palette to reflect the value of ARI_fnc it leads to by way of clustering with k-means. The point leading to the highest ARI_fnc value is marked by the crosshair in the panel. Each right panel provides a view of how ARI_fnc is distributed over all pertaining trials.

Fig 3

Reference partition for the Iris data set (leftmost column of panels) and the effects of two scaling schemes: Scaling by 1/σ_k (middle column) and scaling by α_k/σ_k (rightmost column), with factors as in Table 3. Effects can be seen both with respect to the shape of the data set (top row of panels, all plots drawn to the same scale) and to the distribution of distances between samples (the r_ij’s; bottom row, all plots drawn to the same scale).

Fig 4. As in Fig 3, now for the BNA-DR3 data set.