Decoding the hydrodynamic properties of microscale helical propellers from Brownian fluctuations

Abstract

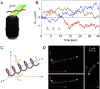
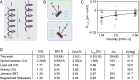
The complex motility of bacteria, ranging from single-swimmer behaviors such as chemotaxis to collective dynamics, including biofilm formation and active matter phenomena, is driven by their microscale propellers. Despite extensive study of swimming flagellated bacteria, the hydrodynamic properties of their helical-shaped propellers have never been directly measured. The primary challenges to directly studying microscale propellers are 1) their small size and fast, correlated motion, 2) the necessity of controlling fluid flow at the microscale, and 3) isolating the influence of a single propeller from a propeller bundle. To solve the outstanding problem of characterizing the hydrodynamic properties of these propellers, we adopt a dual statistical viewpoint that connects to the hydrodynamics through the fluctuation-dissipation theorem (FDT). We regard the propellers as colloidal particles and characterize their Brownian fluctuations, described by 21 diffusion coefficients for translation, rotation, and correlated translation-rotation in a static fluid. To perform this measurement, we applied recent advances in high-resolution oblique plane microscopy to generate high-speed volumetric movies of fluorophore-labeled, freely diffusing Escherichia coli flagella. Analyzing these movies with a bespoke helical single-particle tracking algorithm, we extracted trajectories, calculated the full set of diffusion coefficients, and inferred the average propulsion matrix using a generalized Einstein relation. Our results provide a direct measurement of a microhelix's propulsion matrix and validate proposals that the flagella are highly inefficient propellers, with a maximum propulsion efficiency of less than 3%. Our approach opens broad avenues for studying the motility of particles in complex environments where direct hydrodynamic approaches are not feasible.

Keywords: Brownian motion; E. coli flagella; fluctuation–dissipation theorem; oblique plane microscopy; propulsion matrix.

Fig. 1.

Evaluation of hydrodynamics at low Reynolds number. Top: (A) An individual spherical particle is bombarded by fluid molecules (orange arrows) due to thermal fluctuations k_BT, resulting in Brownian motion (2). (B) An individual flagellum is bombarded by fluid molecules (orange arrows) due to thermal fluctuations k_BT, resulting in Brownian motion, with the fluid surrounding the helix mediating the interaction between translation and rotation (blue arrows). (C) A living E. coli trapped in an optical tweezer generating a torque T_ψ in response to a given fluid flow U_∞, at Re ≈ 10⁻⁴, produces a bead displacement Δz equivalent to a force value around 1 pN (14). (D) A motor generates torque T_ψ on the end of a millimeter-helical wire in a Re ≈ 10⁻³ fluid, causing the helix to rotate at a rate of ω and to produce a force F of ∼100 mN, as measured by a load cell (16). (E) A millimeter-scale wire free-falls in corn syrup medium, at Re ≈ 10⁻¹, subjected to a gravitational force F of about 10 mN. Bottom: Applied force and length scales for each experimental approach.

Fig. 2.

3D tracking of diffusing flagella using an oblique plane light sheet microscope. (A) Schematic of oblique plane light sheet microscope imaging a stained flagellum extracted from E. coli. The light sheet rapidly scanned through the sample to image a 3D volume. (B) Representative center-of-mass displacement tracks along the lab axes for a diffusing flagellum. (C) Illustration of the three unit vectors (${\widehat{\mathbf{n}}}_1,{\widehat{\mathbf{n}}}_2,{\widehat{\mathbf{n}}}_3$) that describe the arbitrary helix orientation relative to the lab axes (x, y, z). (D) Orthographic projections of a 3D image of a single flagellum. Yellow circles and boxes indicate the same flagellum ends in three orthogonal views. Images are shown with a gamma of 0.75.

Fig. 3.

Diffusion coefficients along 6 degrees of freedom for flagella in different viscosity solutions. (A) Representative MSDs for displacement along the longitudinal (purple) and transverse (orange and green) axes. Solid lines are linear fits to the first ten data points. (B and C) Representative MSADs for rotation along the longitudinal (purple) and transverse (orange and green) axes. (D) Translational diffusion coefficients along the longitudinal (purple) and transverse (orange and green) axes for indicated viscosities. (E and F) Rotational diffusion coefficients about the transverse (purple) and longitudinal (orange and green) axes. Diffusion coefficients determined from each measurement (circles) and average diffusion coefficients (pluses) are shown. Error bars are the standard error of the mean (SEM). Lines are fits to the expected 1/η viscosity scaling of the diffusion coefficients.

Fig. 4.

Correlation between translation and rotation. (A) Schematic of translation induced by rotation of a left-handed helix in a viscous fluid. Counterclockwise and clockwise rotations cause the helix to move downward (Left) and upward (Right), respectively. (B) Free-body diagram of filament segments in their rest frames while helix rotates clockwise (panel A, Right). Due to the rotation, the segments see fluid flow (blue) in opposite directions. The forces in the horizontal direction cancel, while those in the vertical direction add causing the helix to translate in the ${\widehat{\mathbf{n}}}_1$ direction (upwards). Green and pink insets correspond to the regions shown in A. (C) Codiffusion coefficients, D_n1ψ1, for flagella in different viscosity solutions. Diffusion coefficients determined from each measurement (circles) and average diffusion coefficients (pluses) are shown. Error bars are SEM. (D) Nondimensionalized propulsion matrix elements obtained from Brownian motion versus conventional hydrodynamics experiments for helices with θ ∼ 32°.