Reconciling scaling of the optical conductivity of cuprate superconductors with Planckian resistivity and specific heat

Abstract

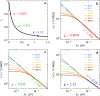
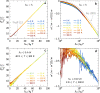
Materials tuned to a quantum critical point display universal scaling properties as a function of temperature T and frequency ω. A long-standing puzzle regarding cuprate superconductors has been the observed power-law dependence of optical conductivity with an exponent smaller than one, in contrast to T-linear dependence of the resistivity and ω-linear dependence of the optical scattering rate. Here, we present and analyze resistivity and optical conductivity of La_2-xSr_xCuO₄ with x = 0.24. We demonstrate ℏω/k_BT scaling of the optical data over a wide range of frequency and temperature, T-linear resistivity, and optical effective mass proportional to [Formula: see text] corroborating previous specific heat experiments. We show that a T, ω-linear scaling Ansatz for the inelastic scattering rate leads to a unified theoretical description of the experimental data, including the power-law of the optical conductivity. This theoretical framework provides new opportunities for describing the unique properties of quantum critical matter.

Fig. 1. Optical data of La_2−xSr_xCuO₄ at p = 0.24.

a Real and b imaginary part of the optical conductivity σ deduced from the dielectric function ϵ (Supplementary Fig. 1), using Eq. (14) and the value ϵ_∞ = 2.76. c Scattering rate and d effective mass deduced from Eqs. (16) and (17) using K = 211 meV. The values of ϵ_∞ and K are discussed and justified in the text. Inset: Temperature dependence of m^*/m at ℏω = 5k_BT (see dots in d). In each panel errorbars are indicated for three representative frequencies and pertain to the upper curve, i.e., the lowest temperature for σ(ω), m^*(ω)/m and the highest temperature for ℏ/τ(ω). They represent the uncertainty arising from reflectivity calibration using in-situ gold evaporation, and have been estimated by repeating the Kramers--Kronig analysis after multiplying the reflectivity curves by 1 ± 0.002.

Fig. 2. Scaling of scattering rate and mass enhancement.

a Temperature-dependent resistivity measured in zero field (black) and at 16 teslas (red). The inset emphasizes the linearity of the 16 T data at low temperature. The dashed line shows ρ₀ + AT with ρ₀ = 12.2 μΩcm and A = 0.63 μΩcm/K. b Scattering rate divided by temperature plotted versus ω/T; the collapse of the curves indicates a behavior 1/τ ~ Tf_τ(ω/T). c Effective quasiparticle mass (in units of the indicated band mass m) deduced from the low-temperature electronic specific heat [$m_{\mathrm{Cp}}^{*}=\left(3/\pi \right)\left({\hslash }^2{d}_c/k_{\mathrm{B}}^2\right)\left(C/T\right)$] and zero-frequency optical mass enhancement; the dashed lines indicate $lnT$ behavior. d Optical mass minus the zero-frequency mass shown in c plotted versus ω/T; the collapse of the curves indicates a behavior m^*(ω) − m^*(0) ~ f_m(ω/T). The data between 0.22 and 0.4 eV are shown as dotted lines. ϵ_∞ = 2.76 was used here as in Fig. 1.

Fig. 3. Sub-linear power law at intermediate frequencies.

a Modulus and b phase of the complex conductivity shown in Fig. 1a and b; the modulus decays with an exponent ν^* ≈ 0.8 and the phase approaches a value slightly lower than (π/2)ν^*. c and d: same quantities calculated using a Planckian model with linear-in-energy scattering rate, Eqs. (7) and (10). The model and parameters are discussed in the text.

Fig. 4. Effective exponent.

Emergence of an apparent sub-linear power-law in a pure Planckian model. a Apparent exponent given by Eq. (12) versus interaction strength g. b–d Modulus of the optical conductivity on a log-log scale showing the apparent power law at energies between k_BT and the cutoff Λ = 0.4 eV. Data are shown for three values of g (dots in a) and a range of temperatures. Both horizontal and vertical axes cover exactly two decades, such that a 1/ω behavior would correspond to a slope of − 1 (dotted line).

Fig. 5. Frequency-temperature scaling.

a Approximate collapse of the theoretical scattering rate and b mass enhancement; the dashed lines show 2πgS(x/2) in a and Eq. (S16) in b. c Same data as in Fig. 2b. d Same data as in Fig. 2d on a logarithmic scale (not displayed here because of excessive noise: ℏω/k_BT < 10 for T < T_c); the dashed line is Eq. (S16).