Asymptotic Distribution of Certain Types of Entropy under the Multinomial Law

Abstract

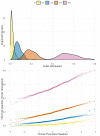
We obtain expressions for the asymptotic distributions of the Rényi and Tsallis of order q entropies and Fisher information when computed on the maximum likelihood estimator of probabilities from multinomial random samples. We verify that these asymptotic models, two of which (Tsallis and Fisher) are normal, describe well a variety of simulated data. In addition, we obtain test statistics for comparing (possibly different types of) entropies from two samples without requiring the same number of categories. Finally, we apply these tests to social survey data and verify that the results are consistent but more general than those obtained with a χ2 test.

Keywords: asymptotic distributions; entropy; hypothesis tests; multinomial distribution.

Figure 1

Linear, One-Almost-Zero, and Half-and-Half probability functions for $k=6$ and $ϵ=0.3$.

Figure 2

Empirical densities and normal QQ-plots of the Fisher information in situations that fail to pass the normality test at 1%.

Figure 3

Examples of cases where the null hypothesis of the Kolmogorov–Smirnov test is rejected. The histograms are computed with samples of size 300 using the Freedman–Diaconis rule [15], and the green lines are the asymptotic probability density functions. (a) Type: $H_S$, Model: OAZ, $k=120$, $n={10}^{4}k$, $p-\mathrm{val}=0.00202$; (b) Type: $H_F$, Model: OAZ, $k=120$, $n={10}^{4}k$, $p-\mathrm{val}=0.00013$; (c) Type: $H_R^{1/3}$, Model: Linear, $k=24$, $n={10}^{4}k$, $p-\mathrm{val}\approx 0$; (d) Type: $H_T^{1/2}$, Model: HaH, $ϵ=0.8$, $k=6$, $n={10}^{4}k$, $p-\mathrm{val}=0.04297$.