Advanced Tree-Based Techniques for Predicting Unconfined Compressive Strength of Rock Material Employing Non-Destructive and Petrographic Tests

Abstract

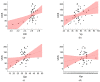
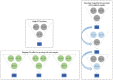
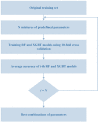
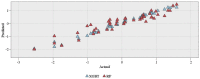
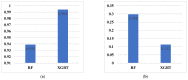
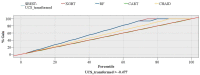
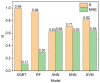
The accurate estimation of rock strength is an essential task in almost all rock-based projects, such as tunnelling and excavation. Numerous efforts to create indirect techniques for calculating unconfined compressive strength (UCS) have been attempted. This is often due to the complexity of collecting and completing the abovementioned lab tests. This study applied two advanced machine learning techniques, including the extreme gradient boosting trees and random forest, for predicting the UCS based on non-destructive tests and petrographic studies. Before applying these models, a feature selection was conducted using a Pearson's Chi-Square test. This technique selected the following inputs for the development of the gradient boosting tree (XGBT) and random forest (RF) models: dry density and ultrasonic velocity as non-destructive tests, and mica, quartz, and plagioclase as petrographic results. In addition to XGBT and RF models, some empirical equations and two single decision trees (DTs) were developed to predict UCS values. The results of this study showed that the XGBT model outperforms the RF for UCS prediction in terms of both system accuracy and error. The linear correlation of XGBT was 0.994, and its mean absolute error was 0.113. In addition, the XGBT model outperformed single DTs and empirical equations. The XGBT and RF models also outperformed KNN (R = 0.708), ANN (R = 0.625), and SVM (R = 0.816) models. The findings of this study imply that the XGBT and RF can be employed efficiently for predicting the UCS values.

Keywords: gradient boosting tree; non-destructive tests; physical properties; random forest; regression tree techniques; rock strength prediction.

Figure 1

Process of this study.

Figure 2

Simple empirical regression models for predicting UCS. (a) UCS = 187.66 $\times$ DD − 386.02; R² = 0.2136; (b) UCS = 0.0163 $\times$ Vp + 15.989; R² = 0.1301; (c) UCS = 2.8535 $\times$ Qtz + 11.013; R² = 0.0998; (d) UCS = 1.7699 $\times$ Kpr + 46.883; R² = 0.0342; (e) UCS = −1.5152 $\times$ Plg + 143.7; R² = 0.0539; (f) UCS = −6.718 $\times$ Chl + 110.84; R² = 0.0469; (g) UCS = −3.563 $\times$ Mica + 129.63; R² = 0.0611.

Figure 2

Simple empirical regression models for predicting UCS. (a) UCS = 187.66 $\times$ DD − 386.02; R² = 0.2136; (b) UCS = 0.0163 $\times$ Vp + 15.989; R² = 0.1301; (c) UCS = 2.8535 $\times$ Qtz + 11.013; R² = 0.0998; (d) UCS = 1.7699 $\times$ Kpr + 46.883; R² = 0.0342; (e) UCS = −1.5152 $\times$ Plg + 143.7; R² = 0.0539; (f) UCS = −6.718 $\times$ Chl + 110.84; R² = 0.0469; (g) UCS = −3.563 $\times$ Mica + 129.63; R² = 0.0611.

Figure 3

Application of bagging and boosting in DTs.

Figure 4

A ten-fold cross-validation procedure.

Figure 5

Process of grid search in this study.

Figure 6

Real vs. predicted values of XGBT and RF.

Figure 7

The performance of the RF and XGBT models. (a) R; (b) MAE.

Figure 8

Gains chart of the models developed in this study.

Figure 9

Models’ comparison.