Evolution of channel flow and Darcy's law beyond the critical Reynolds number

Abstract

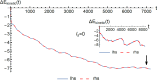
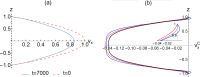
For incompressible channel flow, there is a critical state, characterized by a critical Reynolds number Re_c and a critical wavevector m_c along the channel direction, beyond which the channel flow becomes unstable in the linear regime. In this work, we investigate the channel flow beyond the critical state and find the existence of a new fluctuating, quasi-stationary flow that comprises the laminar Poiseuille flow superposed with a counter-flow component, accompanied by vortices and anti-vortices. The net flow rate is reduced by ~ 15% from the linear, laminar regime. Our study is facilitated by the analytical solution of the linearized, incompressible, three-dimensional (3D) Navier-Stokes (NS) equation in the channel geometry, with the Navier boundary condition, alternatively denoted as the hydrodynamic modes (HMs). By using the HMs as the complete mathematical basis for expanding the velocity in the NS equation, the Re_c is evaluated to 5-digit accuracy when compared to the well-known Orszag result, without invoking the standard Orr-Sommerfeld equation. Beyond Re_c, the analytical solution is indispensable in offering physical insight to those features of the counter-flow component that differs from any of the pressure-driven channel flows. In particular, the counter flow is found to comprise multiple HMs, some with opposite flow direction, that can lead to a net boundary reaction force along the counter-flow direction. The latter is analyzed to be necessary for satisfying Newton's law. Experimental verification of the predictions is discussed.

Fig. 1

Illustration of a antisymmetric 3D HM, b symmetric 3D HM, c antisymmetric 2D HM, d symmetric 2D HM, e antisymmetric 1D HM, and f symmetric 1D HM. The relevant eigenvalue and eigenvector values are below each figure

Fig. 2

Plot of ${\mathrm{Re}}_{\mathrm{c}}$ as a function of the eigen-wavevectors $m_c,k$. The conventional definition of ${\mathrm{Re}}_{\mathrm{c}}$ = 5772.2 is noted to be the minimum point of the discretized curve (i.e., the least stable mode), labeled by a red dot. Here k is an input parameter

Fig. 3

A plot of the critical wavevector $m_c(\mathrm{black})$ and the critical Reynolds number ${\mathrm{Re}}_{\mathrm{c}}(\mathrm{blue})$, both as a function of the slip length $l_s$. Here the Poiseuille flow rate is allowed to vary with the slip length as stipulated by Eq. (1.3b)

Fig. 4

A plot of the normalized net flow rate, in unit of $Q^P$, as a function of time $t$. The time evolution is evaluated from Eq. (3.3) and Eq. (5.3), with the Reynolds number set at Re = 10⁴ for both the slip and nonslip case. The ensemble-averaged net flow rate, with ten independently generated initial states, is seen to decrease as a function of time from the initial Poiseuille flow rate. The yellow curve, indicative of the case for the finite slip length, is seen to approach the equilibrium flow rate slower than that of the nonslip case

Fig. 5

The ensemble-averaged kinetic energy as evaluated from the energy conservation relation Eq. (5.4), plotted as a function of time $t$. Here the kinetic energy is numerically time-integrated from Eq. (5.4). The blue line indicates the left-hand side of Eq. (5.4), and the red dashed line indicates the right-hand side. The nonslip boundary condition was used in this case. The same quantity for a single trajectory is plotted in the inset. It is seen that the energy conservation law is very well obeyed in the time evolution, and the kinetic energy decreases as a function of time, until it reaches a plateau. The vertical arrow indicates the time, t = 7000, at which the flow profile is plotted in Fig. 6

Fig. 6

a Flow profile at two time instances, where v_x denotes the total velocity. At t = 0, the profile is parabolic, corresponding to the Poiseuille flow. At t = 7000, the net flow rate is decreased, even though the profile is still very similar. b The counter-flow profile $v_x^c$ at three time instances, obtained by subtracting off the Poiseuille profile from the total flow profile. The inset shows an enlarged view of the velocity profile in the vicinity of the solid boundary. The counter flow profile can be expressed as a superposition of the 1D symmetric modes, not all flowing along the same direction. It is noted that the boundary reaction force is in the negative x direction at t = 7000 (blue curve). At other two time instances, t = 7560 (red) and t = 7345 (black), the boundary reaction force is either along the positive x direction or nearly zero, respectively. The fluctuating boundary profile as a function of time has a direct bearing on the time-averaged frictional reaction force from the solid boundary arising from $v_x^c$. The blue curve is representative of almost all the counter flow profiles prior to t = 7000

Fig. 7

a A plot of the normalized inertial force and the boundary reaction force as a function of time. The time period is chosen to be in the near-equilibrium state, i.e., after t = 7000. The blue dots denote the inertial force, and the red curve denotes the boundary reaction force. Complete agreement is seen, since the two represent the two sides of the same equation. The black dashed line represents the time average of the boundary reaction force. It is very close to zero. b The $v_x^C$ profile time-averaged over the same time period as shown in (a). The inset shows an enlarge picture of the profile in the vicinity of the boundary. It is seen that ${\left[\frac{\partial v_x^C}{\partial z}\right]}_{z=\pm 1}\approx 0$, indicating a near-zero boundary reaction force in the time-averaged sense