Traces of electron-phonon coupling in one-dimensional cuprates

Abstract

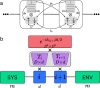
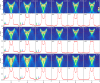
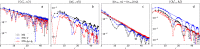
The appearance of certain spectral features in one-dimensional (1D) cuprate materials has been attributed to a strong, extended attractive coupling between electrons. Here, using time-dependent density matrix renormalization group methods on a Hubbard-extended Holstein model, we show that extended electron-phonon (e-ph) coupling presents an obvious choice to produce such an attractive interaction that reproduces the observed spectral features and doping dependence seen in angle-resolved photoemission experiments: diminished 3k_F spectral weight, prominent spectral intensity of a holon-folding branch, and the correct holon band width. While extended e-ph coupling does not qualitatively alter the ground state of the 1D system compared to the Hubbard model, it quantitatively enhances the long-range superconducting correlations and suppresses spin correlations. Such an extended e-ph interaction may be an important missing ingredient in describing the physics of the structurally similar two-dimensional high-temperature superconducting layered cuprates, which may tip the balance between intertwined orders in favor of uniform d-wave superconductivity.

Fig. 1. Schematics for the model and dynamical LBO.

a Schematic for the one-dimensional Hubbard-extended Holstein model. On each site, the local Hilbert space is a direct product of phonon and charge degrees of freedom. The charges of opposite spin interact with an on-site repulsion U and can hop to neighboring sites. Local phonons with a frequency ω₀ couple to both on-site and nearest-neighbor charges. b Schematic for the dynamical LBO. We keep the dimension of the effective Hilbert space of the system and environment blocks as m, respectively. Each site i has an optimized basis of dimension d. The wave function is transformed to a D ≫ d bare basis (D = D_ch × D_ph, where D_ch = 4 represents the local charge Hilbert space dimension, and D_ph is the bare phonon basis dimension) through a D × d transformation matrix, i.e.T_i, before applying the time evolution gate of shape D² × D². Subsequently, a new optimal basis and transformation T_i are obtained; and the wave function is projected to the new optimal basis before moving on to the next gate.

Fig. 2. Single-particle spectral function of Hubbard model at half-filling.

a The lesser Green’s function ${\mathcal{G}}_{j,L/2,\uparrow }^{<}\left(t\right)$ for an 80-site chain at half-filling for the Hubbard model. Time is measured in units of ℏ/t_h and ℏ = 1 in our calculation. We use a time step $\delta t=0.04t_h^{-1}$ and evolve the system for a total time $T=20t_h^{-1}$. b The single-particle spectral function obtained by Fourier transform of ${\mathcal{G}}^{<}$ in (a), with energy and momentum broadening of σ_ω = 0.2t_h and σ_k = 2π/L, respectively.

Fig. 3. Single-particle spectra for different models.

a The Hubbard model (HM), c the extended Hubbard model (HM + V), and e the Hubbard-extended Holstein model (HM + g₀ + g₁), with increasing doping from columns 1–6. Panels b, d, f show representative momentum distribution curves (MDCs), corresponding to the cuts given by the red dashed line for each of the spectra in (a, c, e), respectively. The MDCs are chosen ~t_h above the bottom of the holon branch to ensure that the main holon peaks are at roughly the same position for different dopings and for different models, providing equivalent MDCs for comparison. The green and blue arrows mark the positions of the 3k_F and hf branches, respectively. One can clearly see that at lower doping (<20%), adding nearest neighbor attraction V or extended e–ph coupling can enhance the hf branch while suppressing the 3k_F branch. Above 20% doping, both peaks fade away quickly. Here, the energy and momentum broadening of the spectra are σ_ω = 0.18t_h and σ_k = 2π/L. The lesser Green’s functions data corresponding to all the single-particle spectral functions displayed here can be found in Fig. S5 in Supplementary Information.

Fig. 4. Comparison of experimental and simulated holon binding energy at momentum k = 0.

The experiment data (open circle) are taken from ref. . We use the broadening as the error bar for the simulated data. For the holon binding energy, the Hubbard-extended Holstein model (open square) matches the experiment data very well, while the extended-Hubbard model (open diamond) deviates from the experiment at higher doping. Here we take t_h = 530 meV.

Fig. 5. Correlation functions for different models.

a Single-particle Green’s function. b Spin-spin correlation. c Charge density–density fluctuation correlation. d Spin-singlet superconducting pair-field correlation. Correlations for the Hubbard (black) and extended Hubbard (blue) models are plotted for comparison. The Hubbard-extended Holstein model (red) results were obtained for ω₀ = 0.2t_h, g₀ = 0.3t_h, and g₁ = 0.15t_h. The straight line fits follow a power law decay ~r^−K to extract effective Luttinger exponents for different correlation functions. Filled circles show data used for fitting.