Odd-even disparity in the population of slipped hairpins in RNA repeat sequences with implications for phase separation

Abstract

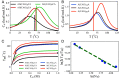
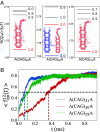
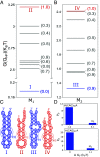
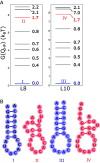
Low-complexity nucleotide repeat sequences, which are implicated in several neurological disorders, undergo liquid-liquid phase separation (LLPS) provided the number of repeat units, n, exceeds a critical value. Here, we establish a link between the folding landscapes of the monomers of trinucleotide repeats and their propensity to self-associate. Simulations using a coarse-grained Self-Organized Polymer (SOP) model for (CAG)_n repeats in monovalent salt solutions reproduce experimentally measured melting temperatures, which are available only for small n. By extending the simulations to large n, we show that the free-energy gap, ΔG_S, between the ground state (GS) and slipped hairpin (SH) states is a predictor of aggregation propensity. The GS for even n is a perfect hairpin (PH), whereas it is a SH when n is odd. The value of ΔG_S (zero for odd n) is larger for even n than for odd n. As a result, the rate of dimer formation is slower in (CAG)₃₀ relative to (CAG)₃₁, thus linking ΔG_S to RNA-RNA association. The yield of the dimer decreases dramatically, compared to the wild type, in mutant sequences in which the population of the SH decreases substantially. Association between RNA chains is preceded by a transition to the SH even if the GS is a PH. The finding that the excitation spectrum-which depends on the exact sequence, n, and ionic conditions-is a predictor of self-association should also hold for other RNAs (mRNA for example) that undergo LLPS.

Keywords: RNA–RNA association; excited states; liquid–liquid phase separation; low complexity RNA sequences; self-organized polymer model.

Fig. 1.

Thermodynamics of (CAG)_n sequences: (A) Heat capacity, C_v, as a function of temperature, T, for G(CAG)₅C (black), G(CAG)₆C (red), and G(CAG)₇C (green) lines. The solid lines correspond to the experimental melting temperatures, T_Ms. (B) Same as (A) except that the plots are for (CAG)₁₄, (CAG)₁₅, and (CAG)₂₀ are in blue, cyan, and magenta lines, respectively. The experimental value for T_M for (CAG)₂₀ is shown as a solid line. (C) Predictions of T_Ms as a function of C_s for G(CAG)_nC for various n that are indicated in the plot. The symbols are the measured values. (D) Log–Log plot of $\frac{\mathrm{\Delta }{T}_M}{T_M}$ (ΔT_M is the full width at half maximum in C_v(T)) as a function of the number of nucleotides, N_T. The slope of the line is ≈0.92, which is close to the expected value of unity based on thermodynamic considerations.

Fig. 2.

Characterizing the hairpin-like structures: (A) Distribution, P(Q_HP), of the order parameter Q_HP, for (CAG)₁₄, (CAG)₂₀, and (CAG)₃₀. The maximum in P(Q_HP) is at Q_HP = 0, implying that the ground state is a PH. (B) Same as (A), except that P(Q_HP)s are shown for odd values of n. The ground states have one unit of slippage, resulting in Q_HP = 1. (C) Representative hairpin structures with different Q_HP for (CAG)₁₄ as an example. (D) The most populated states along with the Q_HP values for (CAG)₁₅. Structures with fractional Q_HP are displayed in SI Appendix.

Fig. 3.

Link between free-energy spectra and the kinetics of dimerization: (A) Free-energy spectra for (CAG)₂₉ (Left), (CAG)₃₀ (Middle), and (CAG)₃₁ (Right) computed at C_s = 0.1 M and T = 37 °C. The value of Q_HP in the ground state for the even sequence is zero, whereas it is unity for the odd sequences. (B) Time-dependent increase in the fraction of interchain base pairs, $f_{\mathit{bp}}^{12}(t)$ upon dimerization for (CAG)₂₉ (green), (CAG)₃₀ (red), and (CAG)₃₁ (blue). (CAG)₂₉ and (CAG)₃₁ dimers form nearly 5 times faster than the (CAG)₃₀ dimer, showing that the differences are not due to minor length difference, but it is an odd–even effect. Initially (at t = 0), the chains are in their ground state.

Fig. 4.

Major dimerization pathway formation for (CAG)₃₁: (A) Time-dependent changes showing loss of fractions of intrachain base pairs (f_bp¹(t) and f_bp²(t)) and gain in interchain base pairs ($f_{\mathit{bp}}^{12})(t)$) in the dominant pathway. The initial structures for both the chains correspond to their ground states (Q_HP = 1). The value of C_s is 100 mM, and T = 37°. The panel below zooms in on the time range where the dimer forms. (B–D) Initial hairpin conformations first transition to the structures with a slipped ends at the termini. The hairpins with the slipped end start interacting with each other and eventually lead to the formation of a dimer through a sequence of transitions. Representative structures along the pathways are shown. Structural transitions in the minor pathway (SI Appendix, Fig. S11).

Fig. 5.

Effect of mutations on dimer yields: (A) Free-energy spectrum of M1 mutant (A(CCG)(CAG)₂₈(CGG)A). The numbers represent the values of Q_HP. (B) Same as (A) except that the folding landscape is for M2 (A(CCG)(CAG)₂₉(CGG)A). The free energy between the ground state (PH) and the SH in M1 is higher than in M2. (C) Schematic structures of the relevant states (I, II, III, and IV) involved in dimer formation. (D) Dimer yields, expressed as percentage, for A(CAG)₃₀A and M1 mutant are in the Top panel, and the Bottom panels show A(CAG)₃₁A and M2. Note that the WT yield is higher in A(CAG)₃₁A than in A(CAG)₃₀A.

Fig. 6.

Free-energy spectra and relevant structures for L8 and L10 hairpins: (A) Calculated spectra for hairpins with heterogeneity in the sequences. The free energies of the aggregation-prone states (in red) are separated from the ground states by about 8k_BT, making the populations of such states vanishingly small. States with Q_HP < 1.7 do not have any slippage. (B) The ground state structures with 5′ and 3′ ends in proximity are in blue. The high free-energy states, with slipped nucleotides, are in red.