A case study of an individual participant data meta-analysis of diagnostic accuracy showed that prediction regions represented heterogeneity well

Abstract

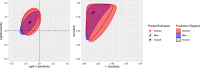
The diagnostic accuracy of a screening tool is often characterized by its sensitivity and specificity. An analysis of these measures must consider their intrinsic correlation. In the context of an individual participant data meta-analysis, heterogeneity is one of the main components of the analysis. When using a random-effects meta-analytic model, prediction regions provide deeper insight into the effect of heterogeneity on the variability of estimated accuracy measures across the entire studied population, not just the average. This study aimed to investigate heterogeneity via prediction regions in an individual participant data meta-analysis of the sensitivity and specificity of the Patient Health Questionnaire-9 for screening to detect major depression. From the total number of studies in the pool, four dates were selected containing roughly 25%, 50%, 75% and 100% of the total number of participants. A bivariate random-effects model was fitted to studies up to and including each of these dates to jointly estimate sensitivity and specificity. Two-dimensional prediction regions were plotted in ROC-space. Subgroup analyses were carried out on sex and age, regardless of the date of the study. The dataset comprised 17,436 participants from 58 primary studies of which 2322 (13.3%) presented cases of major depression. Point estimates of sensitivity and specificity did not differ importantly as more studies were added to the model. However, correlation of the measures increased. As expected, standard errors of the logit pooled TPR and FPR consistently decreased as more studies were used, while standard deviations of the random-effects did not decrease monotonically. Subgroup analysis by sex did not reveal important contributions for observed heterogeneity; however, the shape of the prediction regions differed. Subgroup analysis by age did not reveal meaningful contributions to the heterogeneity and the prediction regions were similar in shape. Prediction intervals and regions reveal previously unseen trends in a dataset. In the context of a meta-analysis of diagnostic test accuracy, prediction regions can display the range of accuracy measures in different populations and settings.

Figure 1

Forest plots of sensitivity (TPR) and specificity (1-FPR). (1) The dotted lines in the sensitivity forest plots indicate that the data from the study indicated a 100% true positive rate and a 0% false positive rate. This caused the sensitivity estimate to be 1 but the standard error was large enough to cover the whole interval $(0,1)$. (2) Red dot-dashed lines indicate the selected cutoff dates for the BREM. (3) Studies are sorted by the year in which the study started, while the label indicates the year in which they were published.)

Figure 2

Prediction and confidence regions through time (FPR = 1 − specificity, TPR = sensitivity). Black dots are the study specific estimates. The red dot is the pooled estimate. The black line indicates the prediction region. The red line is the confidence region. The top panel show the estimates and regions in logit-space, while the bottom panel are in the probability-space. (1) The change in the estimated correlation between sensitivity and 1 − specificity is reflected in the orientation and size of the minor axes of the prediction ellipses in the top row of figure. The orientation of the ellipses relates to the “slope” linking TPR and FPR observations. The strength of the correlation is depicted by the width of the ellipses about their minor axis.)

Figure 3

Prediction regions by sex subgroup (FPR = 1 − specificity, TPR = sensitivity).

Figure 4

Prediction regions by age subgroup (FPR = 1 − specificity, TPR = sensitivity).