Hydration solids
- PMID: 37286609
- PMCID: PMC10530534
- DOI: 10.1038/s41586-023-06144-y
Hydration solids
Abstract
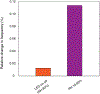
Hygroscopic biological matter in plants, fungi and bacteria make up a large fraction of Earth's biomass1. Although metabolically inert, these water-responsive materials exchange water with the environment and actuate movement2-5 and have inspired technological uses6,7. Despite the variety in chemical composition, hygroscopic biological materials across multiple kingdoms of life exhibit similar mechanical behaviours including changes in size and stiffness with relative humidity8-13. Here we report atomic force microscopy measurements on the hygroscopic spores14,15 of a common soil bacterium and develop a theory that captures the observed equilibrium, non-equilibrium and water-responsive mechanical behaviours, finding that these are controlled by the hydration force16-18. Our theory based on the hydration force explains an extreme slowdown of water transport and successfully predicts a strong nonlinear elasticity and a transition in mechanical properties that differs from glassy and poroelastic behaviours. These results indicate that water not only endows biological matter with fluidity but also can-through the hydration force-control macroscopic properties and give rise to a 'hydration solid' with unusual properties. A large fraction of biological matter could belong to this distinct class of solid matter.
© 2023. The Author(s), under exclusive licence to Springer Nature Limited.
Figures


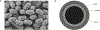

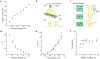

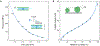


References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

