Generalizing Stepping Concepts To Non-Straight Walking

Abstract

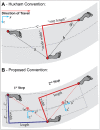
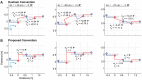
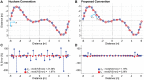
People rarely walk in straight lines. Instead, we make frequent turns or other maneuvers. Spatiotemporal parameters fundamentally characterize gait. For straight walking, these parameters are well-defined for that task of walking on a straight path. Generalizing these concepts to non-straight walking, however, is not straightforward. People also follow non-straight paths imposed by their environment (store aisle, sidewalk, etc.) or choose readily-predictable, stereotypical paths of their own. People actively maintain lateral position to stay on their path and readily adapt their stepping when their path changes. We therefore propose a conceptually coherent convention that defines step lengths and widths relative to known walking paths. Our convention simply re-aligns lab-based coordinates to be tangent to a walker's path at the mid-point between the two footsteps that define each step. We hypothesized this would yield results both more correct and more consistent with notions from straight walking. We defined several common non-straight walking tasks: single turns, lateral lane changes, walking on circular paths, and walking on arbitrary curvilinear paths. For each, we simulated idealized step sequences denoting "perfect" performance with known constant step lengths and widths. We compared results to path- independent alternatives. For each, we directly quantified accuracy relative to known true values. Results strongly confirmed our hypothesis. Our convention returned vastly smaller errors and introduced no artificial stepping asymmetries across all tasks. All results for our convention rationally generalized concepts from straight walking. Taking walking paths explicitly into account as important task goals themselves thus resolves conceptual ambiguities of prior approaches.

Keywords: Goal-Directed Walking; Step Length; Step Width; Stepping; Walking.

Figure 1 –. Defining Stepping Parameters:

A) The convention for defining step length and “stride width” proposed by Huxham et al., 2006. Given only the locations of three consecutive foot placements, the direction of forward progression (DoP) for the middle foot placement is taken as line “c”, which connects the prior and subsequent contralateral foot placements. Huxham’s step lengths ($l_H$) and “stride widths” ($w_H$) are then computed from basic trigonometric relationships: i.e., $l_H=b\cos (\theta )=(b^2+c^2-a^2)∕2c$ and $w_H=\text{sqrt}(b^2-l_H^2)$ (Huxham et al, 2006). Of note, these relationships do not in any way account for where the feet are placed with respect to the walking path. B) The proposed convention presenting a path-based approach for the exact same three foot placements. Each step is considered its own true step, consisting of two foot placements only. The person’s body position is taken as the midpoint between the two foot placements that make up that step (Orendurff et al., 2004; Dingwell & Cusumano, 2019). A local [$x^{\prime },z^{\prime }$] coordinate system is then aligned tangent to the path at the point on the path closest to the body position. Step lengths ($l_P$) and step widths ($w_P$) are then calculated in this path-defined local coordinate system just as they would be in fixed lab-based coordinates for typical straight walking.

Figure 2 –. Different Local Path Coordinate Choices.

When [$x^{\prime },y^{\prime }$] are aligned with the midpoint between the two feet (Fig. 1B), step lengths and step widths are each similar for both steps. However, A) If [$x^{\prime },y^{\prime }$] were instead aligned with the trailing (rear) foot placement of each step, the 1^st (“inside-to-outside”) step becomes longer and narrower, while the 2^nd (“outside-to-inside”) step becomes wider and shorter. B) Conversely, if [$x^{\prime },y^{\prime }$] were aligned with the leading (front) foot placement of each step, the 1^st step now becomes wider and shorter, while the 2^nd step becomes longer and narrower.

Figure 3 –. Single Discrete Turns:

All example sequences shown were constructed to walk from left-to-right, executing a single turn at a single step at the 3^rd step shown. Top and bottom panels show the exact same sequences of steps. A) The Huxham defined “stride widths” ($w_H$) and step lengths ($l_H$) for stepping sequences involving turns executed at a single step. Huxham’s convention returns correct values ($w_H=W;l_H=L$) for all steps before and after the turn (not labeled). However, on the turn step itself, Huxham’s calculations return values that markedly deviate from these. Step width %Errors are +100%, +223%, and −213%, while step length %Errors are −10%, −36%, and −1%, for the 3 turns shown above. These errors scale with the amplitude of turn, despite the fact that the steps themselves (by construction) do not. B) The proposed step lengths ($l_P$) and widths ($w_P$) for the same stepping sequences. Here, because the local [$x^{\prime },z^{\prime }$] coordinate system rotates with the turning movement on the step where the turn is executed, all steps in all sequences stepping return the correct values: i.e., $w_P=W$ and $l_P=L$ for all steps involved in all turns. The proposed methods thus yields 0 %Error for all measures for all steps, regardless of the magnitude of the turn executed.

Figure 4 –. Lateral Lane-Change Maneuvers:

All example sequences shown were constructed to walk from left-to-right, executing a single lateral lane change at a single step after the 2^nd step shown. Top and bottom panels show the exact same sequences of steps. A) The Huxham defined “stride widths” ($w_H$) and step lengths ($l_H$) for stepping sequences involving lateral lane-change maneuvers executed at a single step. Huxham’s convention returns correct values ($w_H=W;l_H=L$) for the first and last steps shown. However, despite that these stepping sequences were explicitly constructed to enact each lane change at a single step, Huxham’s convention necessitates distributing these maneuvers across two consecutive steps. In doing so, Huxham’s calculations return values that markedly deviate from defined movements that generated these lane changes. B) Conversely, the proposed convention keeps the local coordinate system ($[x^{\prime },z^{\prime }]$) at each step aligned to the paths, which in turn change only location and not direction. Thus, all steps in all sequences yield exact step lengths of $l_P=L$. The proposed method likewise yields exact step widths of $w_P=W+\Delta z$ for the step that executes each lane change and $w_P=W$ for all other steps in every sequence. The proposed methods thus yields 0 %Error for all measures for all steps, regardless of the magnitude of the lateral lane change executed.

Figure 5 –. Continuous Walking Around a Circle:

All example sequences shown were constructed to walk in a counter-clockwise direction around each circular path. Top and bottom panels show the exact same sequences of steps. A) The Huxham defined “stride widths” ($w_H$) and step lengths ($l_H$) for each stepping sequence. Because of how $w_H$ and $l_H$ are constructed (Fig. 1A), Huxham’s convention yields markedly different values for outside-to-inside (“out→in”; here, right-to-left) vs. inside-to-outside (“in→out”; here, left-to-right) steps. As shown, the deviations from the correct values ($w_H=W;l_H=L$) increase dramatically as the radius of the circular path ($R_{Path}$) gets smaller. B) The corresponding proposed step widths ($w_P$) and lengths ($l_P$) for the same stepping sequences. Because the proposed convention keeps the local coordinate system ($[x^{\prime },z^{\prime }]$) at each step aligned tangent to the path at that step, and all steps were defined (by construction) equivalently, the proposed method yields the same $w_P$ and $l_P$ values for all steps, both outside-to-inside and inside-to-outside. While these values are not exact (due to approximating curvilinear motion as a straight line within each step), the deviations from the correct (defined) values (i.e., $w_P=W$ and $l_P=L$) are clearly far smaller than for the Huxham convention.

Figure 6 –. Stepping Percent Errors for Walking Around Circles:

A) Percent stepping errors (%Error; Eq. (2), Methods) relative to their prescribed values, plotted versus circular path radius ($R_{Path}$) for both step widths (left) and step lengths (right) for both the Huxham and proposed conventions. Note positive %Errors reflect larger-than-prescribed stepping parameter values, while negative %Errors reflect smaller-than-prescribed stepping parameter values. For very large path radii (i.e., as $R_{Path}\to \infty$), both methods eventually converge to zero (0) %Error for straight walking. However, although %Errors for both methods tend to increase approximately exponentially as $R_{Path}$ gets smaller, these errors are consistently at least ~1-2 orders of magnitude smaller for our proposed convention (Fig. 1B) than for Huxham’s (Fig. 1A). B) Universal Symmetry Index (USI; Eq. (3), Methods) values reflecting relative asymmetries between inside-to-outside and outside-to-inside steps for the data shown in (A). Step widths and step lengths were both highly asymmetrical for the Huxham convention. Conversely, our proposed convention yielded perfectly symmetrical steps (consistent with how the steps were constructed), for all path radii.

Figure 7 –. Stepping Percent Errors vs. [x′,y′] Location For Our Proposed Method:

A) Percent stepping errors (%Error; Eq. (2), Methods) as computed with [$x^{\prime },y^{\prime }$] set at different proportions of the gait cycle, starting from the location of the trailing foot (0; Fig. 2A) to the location of the leading foot (1; Fig. 2B). %Error data are for inside-to-outside (×) and outside-to-inside (○) steps for circular paths of the same path radii as in Fig. 4 (i.e. $R_{Path}=\{6.00,1.50,0.75\}$ m). %Error magnitudes generally increased as [$x^{\prime },y^{\prime }$] was shifted away from the mid-point between the feet (0.5) towards either the trailing foot (0.5 → 0) or leading foot (0.5 → 1). Trends for inside-to-outside steps were opposite to those of outside-to-inside steps. B) Universal Symmetry Index (USI; Eq. (3), Methods) values reflecting relative asymmetries between inside-to-outside and outside-to-inside steps for the data shown in (A). Step widths and step lengths were symmetrical only when [$x^{\prime },y^{\prime }$] was taken at the midpoint between the feet (0.5), and strongly asymmetrical otherwise, especially for step widths.

Figure 8 –. Continuous Walking Along an Arbitrary Path:

A single sequence of 32 consecutive steps was constructed to walk along a curvilinear path defined as a 5^th order polynomial (see Methods). General direction of progression is from left to right. Panels (A) and (B) show the exact same sequences of steps. A) Huxham defined “stride widths” ($w_H$) and step lengths ($l_H$) for this stepping sequence. B) The corresponding proposed step widths ($w_P$) and lengths ($l_P$) for the same stepping sequence. C) %Errors at each step for both step widths (◊) and lengths (○), as computed following the Huxham convention. D) Corresponding %Errors at each step, as computed following the proposed convention. For both methods, the largest errors occurred at points of sharpest curvature, consistent with Figs. 4-5. Across all steps in this sequence, %Errors were consistently ~order-of-magnitude smaller for the proposed convention than for the Huxham convention, also consistent with Figs. 4-5. This was confirmed by computing the median (med) absolute %Error (i.e., −%Error𢈒) across all steps in the sequence, as indicated on each plot.