A Similarity Renormalization Group Approach to Green's Function Methods

Abstract

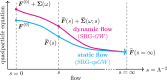
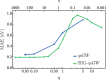
The family of Green's function methods based on the GW approximation has gained popularity in the electronic structure theory thanks to its accuracy in weakly correlated systems combined with its cost-effectiveness. Despite this, self-consistent versions still pose challenges in terms of convergence. A recent study [Monino and Loos J. Chem. Phys. 2022, 156, 231101.] has linked these convergence issues to the intruder-state problem. In this work, a perturbative analysis of the similarity renormalization group (SRG) approach is performed on Green's function methods. The SRG formalism enables us to derive, from first-principles, the expression of a naturally static and Hermitian form of the self-energy that can be employed in quasiparticle self-consistent GW (qsGW) calculations. The resulting SRG-based regularized self-energy significantly accelerates the convergence of qsGW calculations, slightly improves the overall accuracy, and is straightforward to implement in existing code.

Figure 1

Schematic evolution of the quasiparticle equation as a function of the flow parameter s in the case of the dynamic SRG-GW flow (magenta) and the static SRG-qsGW flow (cyan).

Figure 2

Functional form of the qsGW self-energy (left) for η = 1 and the SRG-qsGW self-energy (right) for s = 1/(2η²) = 1/2.

Figure 3

Error [with respect to ΔCCSD(T)] in the principal IP of water in the aug-cc-pVTZ basis set as a function of the flow parameter s for SRG-qsGW (green curve). The HF (cyan line) and qsGW (blue line) values are also reported.

Figure 4

Error [with respect to ΔCCSD(T)] in the principal IP of Li₂, LiH, and the principal EA of F₂ in the aug-cc-pVTZ basis set as a function of the flow parameter s for the SRG-qsGW method (green curves). The HF (cyan lines) and qsGW (blue lines) values are also reported.

Figure 5

Histogram of the errors [with respect to ΔCCSD(T)] for the principal IP of the GW50 test set calculated using HF, G₀W₀@HF, qsGW, and SRG-qsGW. All calculations are performed with the aug-cc-pVTZ basis.

Figure 6

Evolution of the SRG-qsGW (green) and qsGW (blue) MAEs for the principal IPs of the GW50 test set as functions of s and η, respectively. The bottom and top axes are related by s = 1/(2η²). A different marker has been used for qsGW at η = 0.05 because the MAE includes only 48 molecules.

Figure 7

Histogram of the errors [with respect to ΔCCSD(T)] for the principal EA of the GW50 test set calculated using HF, G₀W₀@HF, qsGW, and SRG-qsGW. All calculations are performed with the aug-cc-pVTZ basis.