Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023;32(2):366-377.
doi: 10.1080/10618600.2022.2115500. Epub 2022 Oct 7.

Fast Multilevel Functional Principal Component Analysis

Erjia Cui  1 , Ruonan Li  2 , Ciprian M Crainiceanu  1 , Luo Xiao  2
Affiliations

Fast Multilevel Functional Principal Component Analysis

Erjia Cui et al. J Comput Graph Stat. 2023.

Abstract

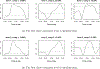
We introduce fast multilevel functional principal component analysis (fast MFPCA), which scales up to high dimensional functional data measured at multiple visits. The new approach is orders of magnitude faster than and achieves comparable estimation accuracy with the original MFPCA (Di et al., 2009). Methods are motivated by the National Health and Nutritional Examination Survey (NHANES), which contains minute-level physical activity information of more than 10000 participants over multiple days and 1440 observations per day. While MFPCA takes more than five days to analyze these data, fast MFPCA takes less than five minutes. A theoretical study of the proposed method is also provided. The associated function mfpca.face() is available in the R package refund.

Keywords: functional principal component analysis; mixed model equations; multilevel models.

PubMed Disclaimer

Figures

Figure 1:
Figure 1:
Physical activity profiles of three NHANES study participants over available days. Each study participant is uniquely identified by the SEQN number. Left column: SEQN 22092. Middle column: SEQN 30209. Right column: SEQN 40757. Within each column, each row displays the minute-level AC of one day from midnight to midnight, titled by day of the week from Sunday (top row) to Saturday (bottom row).
Figure 2:
Figure 2:
Boxplots of estimated eigenvalues from 100 replications when the data are complete with I = 1000, J = 2, L = 100 under unbalanced design for level-1 (first row) and level-2 (second row). True eigenvalues are shown as gray dashed lines, fast MFPCA are shown in red while MFPCA are shown in blue.
Figure 3:
Figure 3:
Estimated eigenfunctions for fast MFPCA (top two rows) and MFPCA (bottom two rows) when the data are complete with I = 1000, J = 2, L = 100 with unbalanced design. Within each model, the top row displays level-1 estimates and the bottom row displays level-2 estimates. Black lines: true eigenfunction; red lines: 100 fast MFPCA estimates; blue lines: 100 MFPCA estimates.
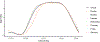
Figure 4:
Figure 4:
Estimated overall mean function μ(s) and day-of-the-week-specific mean function μ(s) + ηj(s) in the NHANES dataset using fast MFPCA. Overall mean curve: black solid line; weekend days means: dashed lines; weekday mean curves: dotted lines.
Figure 5:
Figure 5:
The top three estimated level-1 (first row) and level-2 (second row) eigenfunctions from the NHANES dataset using fast MFPCA. The proportion of variability explained in each principal component within each level is shown on the title of each panel.
See this image and copyright information in PMC

References

    1. Aston JA, Chiou J-M, and Evans JP (2010). Linguistic pitch analysis using functional principal component mixed effect models. Journal of the Royal Statistical Society: Series C (Applied Statistics), 59(2):297–317.
    1. Berrendero JR, Justel A, and Svarc M (2011). Principal components for multivariate functional data. Computational Statistics & Data Analysis, 55(9):2619–2634.
    1. Boland J, Telesca D, Sugar C, Jeste S, Goldbeck C, and Senturk D (2022). A study of longitudinal trends in time-frequency transformations of EEG data during a learning experiment. Computational Statistics & Data Analysis, 167:107367. - PMC - PubMed
    1. Brumback BA and Rice JA (1998). Smoothing spline models for the analysis of nested and crossed samples of curves. Journal of the American Statistical Association, 93(443):961–976.
    1. Chen K and Müller H-G (2012). Modeling repeated functional observations. Journal of the American Statistical Association, 107(500):1599–1609.

LinkOut - more resources