Long-lived metastable knots in polyampholyte chains
- PMID: 37315055
- PMCID: PMC10266668
- DOI: 10.1371/journal.pone.0287200
Long-lived metastable knots in polyampholyte chains
Abstract
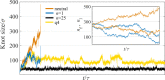
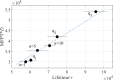
Knots in proteins and DNA are known to have significant effect on their equilibrium and dynamic properties as well as on their function. While knot dynamics and thermodynamics in electrically neutral and uniformly charged polymer chains are relatively well understood, proteins are generally polyampholytes, with varied charge distributions along their backbones. Here we use simulations of knotted polymer chains to show that variation in the charge distribution on a polyampholyte chain with zero net charge leads to significant variation in the resulting knot dynamics, with some charge distributions resulting in long-lived metastable knots that escape the (open-ended) chain on a timescale that is much longer than that for knots in electrically neutral chains. The knot dynamics in such systems can be described, quantitatively, using a simple one-dimensional model where the knot undergoes biased Brownian motion along a "reaction coordinate", equal to the knot size, in the presence of a potential of mean force. In this picture, long-lived knots result from charge sequences that create large electrostatic barriers to knot escape. This model allows us to predict knot lifetimes even when those times are not directly accessible by simulations.
Copyright: © 2023 Ozmaian, Makarov. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

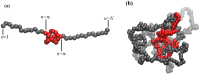

Similar articles
-
Tightness of knots in a polymer chain.Phys Rev E Stat Nonlin Soft Matter Phys. 2010 Apr;81(4 Pt 1):041806. doi: 10.1103/PhysRevE.81.041806. Epub 2010 Apr 26. Phys Rev E Stat Nonlin Soft Matter Phys. 2010. PMID: 20481743 Free PMC article.
-
Quantifying the effects of slit confinement on polymer knots using the tube model.Phys Rev E. 2022 Feb;105(2-1):024501. doi: 10.1103/PhysRevE.105.024501. Phys Rev E. 2022. PMID: 35291068
-
Driving knots on DNA with AC/DC electric fields: topological friction and memory effects.Soft Matter. 2014 Sep 14;10(34):6491-8. doi: 10.1039/c4sm00160e. Soft Matter. 2014. PMID: 25048107
-
Theory of self-contact in Kirchhoff rods with applications to supercoiling of knotted and unknotted DNA plasmids.Philos Trans A Math Phys Eng Sci. 2004 Jul 15;362(1820):1281-99. doi: 10.1098/rsta.2004.1393. Philos Trans A Math Phys Eng Sci. 2004. PMID: 15306451 Review.
-
Knot localization in proteins.Biochem Soc Trans. 2013 Apr;41(2):538-41. doi: 10.1042/BST20120329. Biochem Soc Trans. 2013. PMID: 23514150 Review.
Cited by
-
Polyelectrolytes: From Seminal Works to the Influence of the Charge Sequence.Polymers (Basel). 2023 Nov 30;15(23):4593. doi: 10.3390/polym15234593. Polymers (Basel). 2023. PMID: 38232020 Free PMC article. Review.
-
Energy Landscapes of Model Knotted Polymers.J Chem Theory Comput. 2025 Aug 26;21(16):8168-8181. doi: 10.1021/acs.jctc.5c01005. Epub 2025 Aug 14. J Chem Theory Comput. 2025. PMID: 40810733 Free PMC article.
References
-
- Liu L.F., Depew R.E., and Wang J.C., Knotted single-stranded DNA rings: A novel topological isomer of circular single-stranded DNA formed by treatment with Escherichia coli ω protein. Journal of molecular biology, 1976. 106(2): p. 439–452. - PubMed
-
- Frank-Kamenetskii M., Unraveling DNA: the most important molecule of life. 1997.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

