Analytical solution of l-i SEIR model-Comparison of l-i SEIR model with conventional SEIR model in simulation of epidemic curves

Abstract

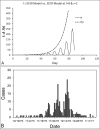
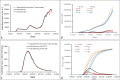
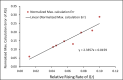
The Susceptible-Exposed-Infectious-Recovered (SEIR) epidemic model has been commonly used to analyze the spread of infectious diseases. This 4-compartment (S, E, I and R) model uses an approximation of temporal homogeneity of individuals in these compartments to calculate the transfer rates of the individuals from compartment E to I to R. Although this SEIR model has been generally adopted, the calculation errors caused by temporal homogeneity approximation have not been quantitatively examined. In this study, a 4-compartment l-i SEIR model considering temporal heterogeneity was developed from a previous epidemic model (Liu X., Results Phys. 2021; 20:103712), and a closed-form solution of the l-i SEIR model was derived. Here, l represents the latent period and i represents the infectious period. Comparing l-i SEIR model with the conventional SEIR model, we are able to examine how individuals move through each corresponding compartment in the two SEIR models to find what information may be missed by the conventional SEIR model and what calculation errors may be introduced by using the temporal homogeneity approximation. Simulations showed that l-i SEIR model could generate propagated curves of infectious cases under the condition of l>i. Similar propagated epidemic curves were reported in literature, but the conventional SEIR model could not generate propagated curves under the same conditions. The theoretical analysis showed that the conventional SEIR model overestimates or underestimates the rate at which individuals move from compartment E to I to R in the rising or falling phase of the number of infectious individuals, respectively. Increasing the rate of change in the number of infectious individuals leads to larger calculation errors in the conventional SEIR model. Simulations from the two SEIR models with assumed parameters or with reported daily COVID-19 cases in the United States and in New York further confirmed the conclusions of the theoretical analysis.

Fig 1. Comparison of difference between the l-i SEIR model and the conventional SEIR model in finding v_{E_out}, the number of people who leave compartment E and enter compartment I per unit time.

Fig 2. Comparison of the number of infectious individuals (I_n) calculated from the l-i SEIR model with the number of infectious individuals (I(t)) calculated from the conventional SEIR model when l>i.

Assuming that the latent period l = 1/σ = 8 days, the infectious period i = 1/γ = 2 days, β_n = β(t) = 1 and N = 3.3x10⁸, the l-i SEIR model generated a propagated epidemic curve for I_n (solid line in A), but the conventional SEIR model generated an epidemic curve for I(t), which increased in a near-exponential form (dashed line in A). Daily measles cases (an example of propagated epidemic curves) were reported in Aberdeen, South Dakota, USA from October 15, 1970 to January 16, 1971 (B).

Fig 3. Examination of differences between curves S(t), E(t), I(t) and R(t) of the conventional SEIR model and their corresponding curves S_n, E_n, I_n and R_n of the l-i SEIR model at different rates of change in the number of infection cases.

Simulations in (A)-(D) were performed by assuming parameters β_n = β(t) = 1 and N = 3.3x10⁸, and (A) l = 1/σ = 2, i = 1/γ = 8, (B) l = 1/σ = 3, i = 1/γ = 7, (C) parameters same as those in (B), but the initial date (the day on which the first person was infected) in the conventional SEIR model was postponed by 3 days, and (D) l = 1/σ = 4, i = 1/γ = 5, the initial date in the conventional SEIR model was postponed by 6 days. (E) Simulations were performed by assuming parameters N = 3.3x10⁸, l = 1/σ = 3, i = 1/γ = 7, and downregulating both β_n and β(t) to slow down I(t) and matching I(t) and I_n to each other. (F) Parameters are the same as those used in (E), but I(t) and I_n were further slowed down by reducing β_n and β(t).

Fig 4. Comparisons of l-i SEIR model with conventional SEIR model in simulations of COVID-19 epidemic data in the US and in NY.

(A) Fitting the numbers of daily new COVID-19 cases (y_n and y(t)) calculated from the two SEIR models to the numbers (red dots) of daily new COVID-19 cases ${\overline{y}}_n$ reported in the United States. (B) The calculated S, E, I and R curves from the two SEIR models after the fitting process in (A) was completed. (C) and (D) are the same as (A) and (B) except that the numbers of daily new COVID-19 cases ${\overline{y}}_n$ were reported in NY.

Fig 5. Plot of the normalized maximal calculation errors of R(t) vs. the relative rising rate of I(t) with data from Table 1.