Evidence for the utility of quantum computing before fault tolerance

Abstract

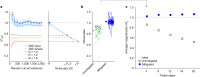
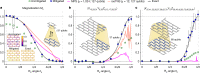
Quantum computing promises to offer substantial speed-ups over its classical counterpart for certain problems. However, the greatest impediment to realizing its full potential is noise that is inherent to these systems. The widely accepted solution to this challenge is the implementation of fault-tolerant quantum circuits, which is out of reach for current processors. Here we report experiments on a noisy 127-qubit processor and demonstrate the measurement of accurate expectation values for circuit volumes at a scale beyond brute-force classical computation. We argue that this represents evidence for the utility of quantum computing in a pre-fault-tolerant era. These experimental results are enabled by advances in the coherence and calibration of a superconducting processor at this scale and the ability to characterize¹ and controllably manipulate noise across such a large device. We establish the accuracy of the measured expectation values by comparing them with the output of exactly verifiable circuits. In the regime of strong entanglement, the quantum computer provides correct results for which leading classical approximations such as pure-state-based 1D (matrix product states, MPS) and 2D (isometric tensor network states, isoTNS) tensor network methods^2,3 break down. These experiments demonstrate a foundational tool for the realization of near-term quantum applications^4,5.

Fig. 1. Noise characterization and scaling for 127-qubit Trotterized time-evolution circuits.

a, Each Trotter step of the Ising simulation includes single-qubit X and two-qubit ZZ rotations. Random Pauli gates are inserted to twirl (spirals) and controllably scale the noise of each CNOT layer. The dagger indicates conjugation by the ideal layer. b, Three depth-1 layers of CNOT gates suffice to realize interactions between all neighbour pairs on ibm_kyiv. c, Characterization experiments efficiently learn the local Pauli error rates λ_l,i (colour scales) comprising the overall Pauli channel Λ_l associated with the lth twirled CNOT layer. (Figure expanded in Supplementary Information IV.A). d, Pauli errors inserted at proportional rates can be used to either cancel (PEC) or amplify (ZNE) the intrinsic noise.

Fig. 2. Zero-noise extrapolation with probabilistic error amplification.

Mitigated expectation values from Trotter circuits at the Clifford condition θ_h = 0. a, Convergence of unmitigated (G = 1), noise-amplified (G > 1) and noise-mitigated (ZNE) estimates of ⟨Z₁₀₆⟩ after four Trotter steps. In all panels, error bars indicate 68% confidence intervals obtained by means of percentile bootstrap. Exponential extrapolation (exp, dark blue) tends to outperform linear extrapolation (linear, light blue) when differences between the converged estimates of ⟨Z₁₀₆⟩_G≠0 are well resolved. b, Magnetization (large markers) is computed as the mean of the individual estimates of ⟨Z_q⟩ for all qubits (small markers). c, As circuit depth is increased, unmitigated estimates of M_z decay monotonically from the ideal value of 1. ZNE greatly improves the estimates even after 20 Trotter steps (see Supplementary Information II for ZNE details).

Fig. 3. Classically verifiable expectation values from 127-qubit, depth-15 Clifford and non-Clifford circuits.

Expectation value estimates for θ_h sweeps at a fixed depth of five Trotter steps for the circuit in Fig. 1a. The considered circuits are non-Clifford except at θ_h = 0, π/2. Light-cone and depth reductions of respective circuits enable exact classical simulation of the observables for all θ_h. For all three plotted quantities (panel titles), mitigated experimental results (blue) closely track the exact behaviour (grey). In all panels, error bars indicate 68% confidence intervals obtained by means of percentile bootstrap. The weight-10 and weight-17 observables in b and c are stabilizers of the circuit at θ_h = π/2 with respective eigenvalues +1 and −1; all values in c have been negated for visual simplicity. The lower inset in a depicts variation of ⟨Z_q⟩ at θ_h = 0.2 across the device before and after mitigation and compares with exact results. Upper insets in all panels illustrate causal light cones, indicating in blue the final qubits measured (top) and the nominal set of initial qubits that can influence the state of the final qubits (bottom). M_z also depends on 126 other cones besides the example shown. Although in all panels exact results are obtained from simulations of only causal qubits, we include tensor network simulations of all 127 qubits (MPS, isoTNS) to help gauge the domain of validity for those techniques, as discussed in the main text. isoTNS results for the weight-17 operator in c are not accessible with current methods (see Supplementary Information VI). All experiments were carried out for G = 1, 1.2, 1.6 and extrapolated as in Supplementary Information II.B. For each G, we generated 1,800–2,000 random circuit instances for a and b and 2,500–3,000 instances for c.

Fig. 4. Estimating expectation values beyond exact verification.

Plot markers, confidence intervals and causal light cones appear as defined in Fig. 3. a, Estimates of a weight-17 observable (panel title) after five Trotter steps for several values of θ_h. The circuit is similar to that in Fig. 3c but with further single-qubit rotations at the end. This effectively simulates the time evolution of the spins after Trotter step six by using the same number of two-qubit gates used for Trotter step five. As in Fig. 3c, the observable is a stabilizer at θ_h = π/2 with eigenvalue −1, so we negate the y axis for visual simplicity. Optimization of the MPS simulation by including only qubits and gates in the causal light cone enables a higher bond dimension (χ = 3,072), but the simulation still fails to approach −1 (+1 in negated y axis) at θ_h = π/2. b, Estimates of the single-site magnetization 〈Z₆₂〉 after 20 Trotter steps for several values of θ_h. The MPS simulation is light-cone-optimized and performed with bond dimension χ = 1,024, whereas the isoTNS simulation (χ = 12) includes the gates outside the light cone. The experiments were carried out with G = 1, 1.3, 1.6 for a and G = 1, 1.2, 1.6 for b, and extrapolated as in Supplementary Information II.B. For each G, we generated 2,000–3,200 random circuit instances for a and 1,700–2,400 instances for b.