Homeostatic regulation of neuronal function: importance of degeneracy and pleiotropy

Abstract

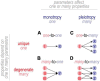
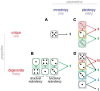
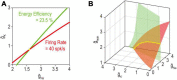
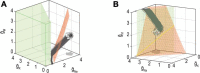
Neurons maintain their average firing rate and other properties within narrow bounds despite changing conditions. This homeostatic regulation is achieved using negative feedback to adjust ion channel expression levels. To understand how homeostatic regulation of excitability normally works and how it goes awry, one must consider the various ion channels involved as well as the other regulated properties impacted by adjusting those channels when regulating excitability. This raises issues of degeneracy and pleiotropy. Degeneracy refers to disparate solutions conveying equivalent function (e.g., different channel combinations yielding equivalent excitability). This many-to-one mapping contrasts the one-to-many mapping described by pleiotropy (e.g., one channel affecting multiple properties). Degeneracy facilitates homeostatic regulation by enabling a disturbance to be offset by compensatory changes in any one of several different channels or combinations thereof. Pleiotropy complicates homeostatic regulation because compensatory changes intended to regulate one property may inadvertently disrupt other properties. Co-regulating multiple properties by adjusting pleiotropic channels requires greater degeneracy than regulating one property in isolation and, by extension, can fail for additional reasons such as solutions for each property being incompatible with one another. Problems also arise if a perturbation is too strong and/or negative feedback is too weak, or because the set point is disturbed. Delineating feedback loops and their interactions provides valuable insight into how homeostatic regulation might fail. Insofar as different failure modes require distinct interventions to restore homeostasis, deeper understanding of homeostatic regulation and its pathological disruption may reveal more effective treatments for chronic neurological disorders like neuropathic pain and epilepsy.

Keywords: degeneracy; excitability; homeostatic regulation; ion channels; pleiotropy; robustness.

FIGURE 1

Negative feedback control. (A) The difference between an output and its set point constitutes an error signal that is used to adjust how the input is processed. Homeostatic adjustments maintain output near its set point despite changes in input; for example, ion channel levels are adjusted to maintain a desired average firing rate despite changes in presynaptic activity. (B) In a more complicated scenario, presynaptic activity (input) is modulated by synaptic strength (gain 1) to yield post-synaptic depolarization (output 1 = input 2), which is, in turn, modulated by intrinsic excitability (gain 2) to yield firing rate (output 2). Here, each dial is controlled independently using separate error signals, but other scenarios are conceivable. Understanding how each loop is organized and whether loops interact is important for appreciating what is being regulated and how.

FIGURE 2

Adjusting excitability supports consistent coding. On a short timescale, variations in input will produce (and be encoded by) variations in output firing. Ideally, the input distribution matches the dynamic range of the system so that the full range of output is used to represent the full range of input. To maintain optimal coding, the input-output transformation (excitability) should adapt to slow changes in the input distribution in order to maintain the output distribution. (A) If the input distribution is compressed (red) or expanded (cyan), gain should increase or decrease, respectively. (B) If the input distribution is shifted left (red) or right (cyan), offset should be shifted left or right, respectively. Notably, different changes in the input call for different homeostatic changes in the transformation.

FIGURE 3

Mapping between parameters and properties. (A) In one-to-one mapping, one parameter affects one property. The basis (or solution) for property X is unique in that it depends only on parameter I. Parameter I is monotropic in that it affects only property X. (B) In many-to-one mapping, the basis for property Y is degenerate in that the same value of Y can be achieved with multiple different combinations of parameters I-III. Individual parameters are still monotropic in that they affect only property Y. (C) In one-to-many mapping, one parameter affects multiple properties. While the basis for properties X-Z is unique, parameter I is pleiotropic in that it affects properties X-Z. In this scenario, adjusting parameter I to regulate property X risks disrupting properties Y and Z. (D) Many-to-many mapping combines degeneracy and pleiotropy. Despite the disruptive consequences of adjusting a pleiotropic channel, there is usually a channel combination that will yield the intended value for all properties because a degenerate property can achieve its intended value using different channel combinations. In this scenario, adjusting one channel is liable to trigger secondary adjustments in many other channels. Degeneracy makes it possible for combined changes to settle on mutually agreeable solutions, thus enabling multiple properties to be co-regulated by adjusting pleiotropic channels.

FIGURE 4

Dice analogies to illustrate mappings in Figure 3. (A) An example of one-to-one mapping is when one die is rolled to produce 5. There is only one way to throw a 5 when using a single die. (B) An example of many-to-one mapping is when two dice are summed to produce 5: 4 + 1 and 2 + 3 are functionally but not structurally redundant and thus constitute degenerate solutions. By comparison, 4 + 1 and 1 + 4 are structurally redundant, and do not constitute degenerate solutions. (C) An example of one-to-many mapping is when one die affects two different arithmetic operations, such as 2 on one die combining with 3 on another to yield 5 (=2 + 3) and 6 (=2 × 3). (D) In many-to-many mapping, multiple dice combine in different ways to produce multiple outcomes. One may recognize this as a system of linear equations, e.g., which combination of dice adds to give X and multiplies to give Y. Each unknown constitutes a degree of freedom and each equation constitutes a constraint. If constraints outnumber degrees of freedom, no solution likely exists and the system is said to be overdetermined. If degrees of freedom outnumber constraints, many solutions likely exist and the systems is therefore undetermined. From the perspective of a homeostatically regulated system, underdetermination is beneficial since any solution giving the desired output is acceptable, and so having many acceptable solutions makes for easier, more robust regulation.

FIGURE 5

Dimensionality of the solution manifold affects the strength of pairwise correlations. For insets in panels (A,B), all parameter combinations producing the desired firing rate of 40 spk/s are shown in red and constitute the solution manifold. The solution manifold corresponds to a curve in panel (A) (1-dimensional) and a surface in panel (B) (2-dimensional). Dots show a set of ion channel combinations initially (white) and after regulation (gray). Other plots summarize distributions of channel densities after regulation. (A) When firing rate is regulated by adjusting just two ion channels, the pairwise correlation is strong because variation in one channel is offset entirely by co-variation in the other channel. (B) When firing rate is regulated by adjusting three channels, pairwise correlations weaken because variation in one channel is offset by variations in two other channels. (C) Pairwise correlations continue to weaken as more adjustable channels are involved. Ion channel correlations may exist despite a high-dimensional solution manifold if the homeostatic regulation maintain correlations despite noise (see text). Modified from Figure 6 of Yang et al. (2022).

FIGURE 6

The solution for multiple properties corresponds to where the individual solutions for each property intersect. (A) When adjusting just two ion channels, the solution manifold for firing rate (red) or energy efficiency (green) each correspond to a curve (1-dimensional). Hence, the joint solution for both properties (yellow) corresponds to where the curves intersect, which occurs at a point (0-dimensional). (B) With three adjustable ion channels (right), the solution for a single property is a surface (2-dimensional); hence, the joint solution for both properties corresponds to a curve (1-dimensional). Please note the connection with overdetermination and underdetermination discussed in Figure 4. Modified from Figure 5 of Yang et al. (2022).

FIGURE 7

Energy efficiency of spike generation depends on overlap between Na⁺ and K⁺ currents. Sample spike evoked by a 17 pA current step applied to a model of a mouse nociceptive sensory neuron that relies on either Na_V1.8 (left) or Na_V1.7 (right). The overlap between Na⁺ and K⁺ currents (middle) corresponds to the amount of “waste” current. Differences in activation (m) and inactivation (h) (bottom) explain differences in the spike waveform and energy efficiency. Na_V1.8 and Na_V1.7 models correspond to models for day in vitro 0 and 4–7, respectively, from Xie et al. (2022).

FIGURE 8

Mechanisms for failing to co-regulate two properties. (A) If the solution manifold for firing rate (red) does not intersect the solution manifold for energy efficiency (green), then no ion channel combinations exist that achieve the target for firing rate and energy efficiency. In other words, solutions for each property exist but are incompatible with one another. In this example, homeostatic regulation found an intermediate, compromise solution. (B) Solution manifolds for different properties may exist and intersect, yet ion channel densities may not reach the joint solution (yellow) because of conflicting adjustments arising from different error signals. Different feedback loops cause solutions to approach the manifold with different trajectories, which may be incompatible. Modified from Figures 9 and 10 of Yang et al. (2022).