Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Jan 10:9:e1195.
doi: 10.7717/peerj-cs.1195. eCollection 2023.

Persistent homology classification algorithm

Mark Lexter D De Lara  1   2
Affiliations

Persistent homology classification algorithm

Mark Lexter D De Lara. PeerJ Comput Sci. .

Abstract

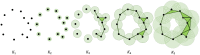
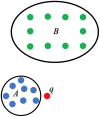
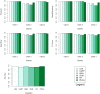
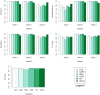
Data classification is an important aspect of machine learning, as it is utilized to solve issues in a wide variety of contexts. There are numerous classifiers, but there is no single best-performing classifier for all types of data, as the no free lunch theorem implies. Topological data analysis is an emerging topic concerned with the shape of data. One of the key tools in this field for analyzing the shape or topological properties of a dataset is persistent homology, an algebraic topology-based method for estimating the topological features of a space of points that persists across several resolutions. This study proposes a supervised learning classification algorithm that makes use of persistent homology between training data classes in the form of persistence diagrams to predict the output category of new observations. Validation of the developed algorithm was performed on real-world and synthetic datasets. The performance of the proposed classification algorithm on these datasets was compared to that of the most widely used classifiers. Validation runs demonstrated that the proposed persistent homology classification algorithm performed at par if not better than the majority of classifiers considered.

Keywords: Classification algorithm; Persistent homology; Supervised learning; Topological data analysis.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no competing interests.

Figures

Figure 1
Figure 1. Filtration of a point cloud into a nested sequence of simplicial complexes, with K1⊆K2⊆...⊆K5.
Figure 2
Figure 2. Point clouds X1, X2, and X3, and point P.
Figure 3
Figure 3. Persistence barcodes corresponding to the 0-dimensional holes in the filtration of the Xi’s and Yi’s.
Figure 4
Figure 4. Training set of points categorized into class A (blue points) and class B (green points), and a new point q.
Figure 5
Figure 5. Barplots of performance metrics of PHCA and the five other classifiers for the iris dataset.
Figure 6
Figure 6. Barplots of performance metrics of PHCA and the five other classifiers for the wheat seeds dataset.
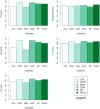
Figure 7
Figure 7. Barplots of performance metrics of PHCA and the five other classifiers for the social network ads dataset.
Figure 8
Figure 8. Barplots of performance metrics of PHCA and the five other classifiers for the synthetic dataset.
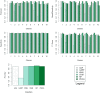
Figure 9
Figure 9. Barplots of performance metrics of PHCA and the five other classifiers for the MNIST dataset.
See this image and copyright information in PMC

References

    1. Abiodun OI, Jantan A, Omolara AE, Dada KV, Mohamed NA, Arshad H. State-of-the-art in artificial neural network applications: a survey. Heliyon. 2018;4(11):e00938. doi: 10.1016/j.heliyon.2018.e00938. - DOI - PMC - PubMed
    1. Alpaydin E. Introduction to machine learning. Third Edition. Cambridge: MIT Press; 2014. (Adaptive Computation and Machine Learning Series).
    1. Carlsson G. Topology and data. Bulletin of the American Mathematical Society. 2009;46(2):255–308. doi: 10.1090/S0273-0979-09-01249-X. - DOI
    1. Carlsson G. Topological pattern recognition for point cloud data. Acta Numerica. 2014;23:289–368. doi: 10.1017/S0962492914000051. - DOI
    1. Charytanowicz M, Niewczas J, Kulczycki P, Kowalski P, Lukasik S, Zak S. A complete gradient clustering algorithm for features analysis of X-ray images

LinkOut - more resources