Unraveling multi-fixel microstructure with tractography and angular weighting

Abstract

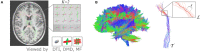
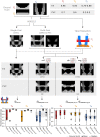
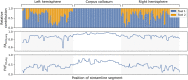
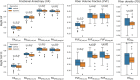
Recent advances in MRI technology have enabled richer multi-shell sequences to be implemented in diffusion MRI, allowing the investigation of both the microscopic and macroscopic organization of the brain white matter and its complex network of neural fibers. The emergence of advanced diffusion models has enabled a more detailed analysis of brain microstructure by estimating the signal received from a voxel as the combination of responses from multiple fiber populations. However, disentangling the individual microstructural properties of different macroscopic white matter tracts where those pathways intersect remains a challenge. Several approaches have been developed to assign microstructural properties to macroscopic streamlines, but often present shortcomings. ROI-based heuristics rely on averages that are not tract-specific. Global methods solve a computationally-intensive global optimization but prevent the use of microstructural properties not included in the model and often require restrictive hypotheses. Other methods use atlases that might not be adequate in population studies where the shape of white matter tracts varies significantly between patients. We introduce UNRAVEL, a framework combining the microscopic and macroscopic scales to unravel multi-fixel microstructure by utilizing tractography. The framework includes commonly-used heuristics as well as a new algorithm, estimating the microstructure of a specific white matter tract with angular weighting. Our framework grants considerable freedom as the inputs required, a set of streamlines defining a tract and a multi-fixel diffusion model estimated in each voxel, can be defined by the user. We validate our approach on synthetic data and in vivo data, including a repeated scan of a subject and a population study of children with dyslexia. In each case, we compare the estimation of microstructural properties obtained with angular weighting to other commonly-used approaches. Our framework provides estimations of the microstructure at the streamline level, volumetric maps for visualization and mean microstructural values for the whole tract. The angular weighting algorithm shows increased accuracy, robustness to uncertainties in its inputs and maintains similar or better reproducibility compared to commonly-used analysis approaches. UNRAVEL will provide researchers with a flexible and open-source tool enabling them to study the microstructure of specific white matter pathways with their diffusion model of choice.

Keywords: diffusion MRI; microstructure; multi-fascicle models; tractography; white matter.

Figure 1

The proposed UNRAVEL framework requires two independent inputs: a multi-fixel microstructural model estimated in the white matter and the streamlines of a given macroscopic tract of interest. (A) 2D slice of a volume with up to K fixels in each voxel obtained with a multi-fixel model (such as DIAMOND [DMD] and Microstructure Fingerprinting [MF]), with each fixel possessing a main orientation (shown as colored sticks) and different microstructural properties. (B) Illustration of a macroscopic tract $\mathcal{T}$, composed of streamlines $\mathcal{L}$ made of segments s. In this illustration, tract $\mathcal{T}$ was isolated from a set of whole-brain tractography streamlines.

Figure 2

Angular weighting attributes a relative weight to all fixels based on the angle difference. Graphical representation of (A) the orientations ${û}_1^{\mu }$ and ${û}_2^{\mu }$ of two fixels and a segment s of a streamline $\mathcal{L}$ in a voxel v. Relative contribution α_vsk of fixel 1 (k = 1, red) and fixel 2 (k = 2, blue) with (B) relative volume weighting, (C) closest-fixel-only, and (D) angular weighting strategies as a function of the orientation û_s of the streamline segment in the voxel.

Figure 3

Different approaches to attribute microstructural properties to macroscopic tracts with our proposed UNRAVEL framework. The ground truth (top row) schematically depicts crossing fascicles of axons (not to scale). The grayscale maps in the background show the value of a tract-specific microstructural metric M. Either a single- or a multi-fixel model (with K = 2 in our example) is estimated (second row). Note that a multi-fixel model does not guarantee a consistent separation of fixels in regions of crossings. The outputs of the proposed method are: (A) Microstructure maps (Equation 9), created for each tract $\mathcal{T}$ using a relative contribution defined by either vol, cfo or ang. (B) The maps are then averaged as a single value (Equation 10) with the roi or tsl option.

Figure 4

The UNRAVEL framework enables more accurate estimation of the tract-specific microstructure, less impacted by tract crossings. Two horizontal tracts ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$ with a high FA and FVF are crossed by vertical tracts ${\mathcal{T}}_3$ with lower FA and FVF. Tract-specific microstructure maps, defined by Equation (9), are shown for the microstructural metrics FA and FVF. Bottom row: the mean (circle), median (dash), and interquartile range (boxes) of FA and FVF values found for each tract are displayed, the average ground truth value is indicated by a continuous gray line while the minimum and maximum values are shown by dashed gray lines.

Figure 5

Angular-weighted relative fixel contribution robustly captures varying microstructure along the course of a single streamline. (A) A single streamline was isolated (in orange) and all its segments were investigated. The local multi-fixel models were (B) DIAMOND (DMD) and (C) Microstructure Fingerprinting (MF), each leading to different fixel orientations in each voxel. The DMD model incorrectly estimated two populations in the top half of the vertical tracts. The (B) FA or (C) FVF values attributed to the streamline segments were computed from the FA or FVF of the multiple fixels in the voxel, following Equation (5). For both (B, C), the values were estimated using the relative volume weighting approach (Equation 2, in blue), closest-fixel-only approach (Equation 3, in red) and the angular weighting approach (Equation 4, in green).

Figure 6

Multi-fixel metrics combined with angular weighting shows smaller variability compared to single-fixel metrics and smaller mean bias compared to relative fraction weighting in a scan/rescan experiment. Bland-Altman plots of the percentage change between the scan and the rescan of, respectively, (A) ${\overline{\mathit{\text{FA}}}}_{\mathrm{\text{DTI}},roi}$ (Mean = 0.11;SD = 1.4), (B) ${\overline{\mathit{\text{FA}}}}_{\mathrm{\text{DMD}},vol,roi}$ (Mean = 0.43; SD = 0.44), (C) ${\overline{\mathit{\text{FA}}}}_{\mathrm{\text{DMD}},\mathit{\text{cfo}},tsl}$ (Mean = −0.27; SD = 0.51) and (D) the proposed ${\overline{\mathit{\text{FA}}}}_{\mathrm{\text{DMD}},ang,tsl}$ (Mean = 0.17;SD = 0.53) from Equation (10) across the 38 considered WM tracts.

Figure 7

The microstructure along a streamline follows macrostructural changes through brain regions with different neural fiber configurations. The evolution of the relative contributions α_vsk of two fixels (in blue and orange) for a single callosal streamline along its path (top). Segment-specific FA_vs (middle) and FVF_vs (bottom) values computed with the UNRAVEL framework using Equation (5).

Figure 8

Estimates of FA and FVF obtained with the UNRAVEL framework suggest values are slightly lower in children with dyslexia compared to controls. Boxplots of the tract-wide mean of the fractional anisotropy (${\overline{\mathit{\text{FA}}}}_{\mathrm{\text{DTI}}}$, ${\overline{\mathit{\text{FA}}}}_{\mathrm{\text{DMD}},vol}$, ${\overline{\mathit{\text{FA}}}}_{\mathrm{\text{DMD}},cfo,tsl}$, ${\overline{\mathit{\text{FA}}}}_{\mathrm{\text{DMD}},ang,tsl}$), fiber volume fraction (${\overline{\mathit{\text{FVF}}}}_{\mathrm{\text{MF}},vol}$, ${\overline{\mathit{\text{FVF}}}}_{\mathrm{\text{MF}},cfo,tsl}$, ${\overline{\mathit{\text{FVF}}}}_{\mathrm{\text{MF}},ang,tsl}$) and the mean of the fiber density maps obtained with the FBA pipeline FD_FBA for the dyslexic (orange) and control (blue) cohort in the right arcuate fasciculus (AF, top) and the right superior longitudinal fasciculus II (SLFII, bottom).

Figure 9

Metrics maps obtained with angular weighting are less impacted by the properties of crossing fibers. Top-left: representation of the streamlines of the left arcuate fasciculus tract, color-coded for orientation. Bottom-left: weighted maps. The tract-specific total segment length map was obtained with Equation (8) and corresponds to the total length of segments belonging to the AF in each voxel. Right: visualization of the microstructure map over a set of 3D streamlines and a 2D slice of the fractional anisotropy obtained with DTI (FA_DTI) and multi-fixel models with: relative volume weighting [FA_{DMD, vol}, see Equation (2)], closest-fixel-only [FA_{DMD, cfo}, see Equation (3)] and our proposed angular weight [FA_{DMD, ang}, see Equation (4)].

Figure 10

Metrics maps using angular weight recover the properties along the direction of the tract. Microstructure maps of the arcuate fasciculus (A, B) and the frontal aslant tract (C, D). (A) Color-coded maps (RGB) of the orientation of the fixel obtained with DIAMOND (DMD) and (C) Microstructure Fingerprinting (MF) are compared to maps obtained with DTI. Microstructural maps of the (B) FA and (D) FVF are also compared to the FA obtained with DTI.