Historical Lattice Trees
- PMID: 37360187
- PMCID: PMC10285026
- DOI: 10.1007/s00220-023-04641-9
Historical Lattice Trees
Abstract
We prove that the rescaled historical processes associated to critical spread-out lattice trees in dimensions converge to historical Brownian motion. This is a functional limit theorem for measure-valued processes that encodes the genealogical structure of the underlying random trees. Our results are applied elsewhere to prove that random walks on lattice trees, appropriately rescaled, converge to Brownian motion on super-Brownian motion.
© The Author(s) 2023.
Conflict of interest statement
Conflict of interestThe authors have no conflict of interest to declare that are relevant to the content of this article.
Figures
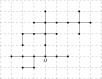

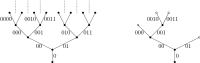

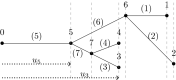
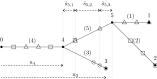

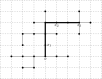


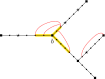
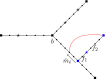
 to
to  and
and  to
to  as indicated
as indicatedReferences
-
- Banova, T.: Convergence of the voter model to historical Brownian motion in dimensions. PhD thesis in progress (2022)
-
- Ben Arous, G., Cabezas, M., Fribergh, A.: The ant on lattice trees. Preprint (2022)
-
- Bramson M, Cox JT, Le Gall J-F. Super-Brownian limits of voter model clusters. Ann. Probab. 2001;29:1001–1032. doi: 10.1214/aop/1015345593. - DOI
-
- Cox JT, Durrett R, Perkins E. Rescaled voter models converge to cuper-Brownian motion. Ann. Probab. 2000;28(1):185–234. doi: 10.1214/aop/1019160117. - DOI
-
- Croydon D. Hausdorff measure of arcs and Brownian motion on Brownian spatial trees. Ann. Probab. 2009;37:946–978. doi: 10.1214/08-AOP425. - DOI
LinkOut - more resources
Full Text Sources
