A computational technique for the Caputo fractal-fractional diabetes mellitus model without genetic factors

Abstract

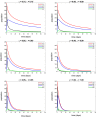
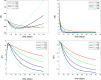
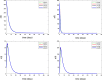
The concept of a Caputo fractal-fractional derivative is a new class of non-integer order derivative with a power-law kernel that has many applications in real-life scenarios. This new derivative is applied newly to model the dynamics of diabetes mellitus disease because the operator can be applied to formulate some models which describe the dynamics with memory effects. Diabetes mellitus as one of the leading diseases of our century is a type of disease that is widely observed worldwide and takes the first place in the evolution of many fatal diseases. Diabetes is tagged as a chronic, metabolic disease signalized by elevated levels of blood glucose (or blood sugar), which results over time in serious damage to the heart, blood vessels, eyes, kidneys, and nerves in the body. The present study is devoted to mathematical modeling and analysis of the diabetes mellitus model without genetic factors in the sense of fractional-fractal derivative. At first, the critical points of the diabetes mellitus model are investigated; then Picard's theorem idea is applied to investigate the existence and uniqueness of the solutions of the model under the fractional-fractal operator. The resulting discretized system of fractal-fractional differential equations is integrated in time with the MATLAB inbuilt Ode45 and Ode15s packages. A step-by-step and easy-to-adapt MATLAB algorithm is also provided for scholars to reproduce. Simulation experiments that revealed the dynamic behavior of the model for different instances of fractal-fractional parameters in the sense of the Caputo operator are displayed in the table and figures. It was observed in the numerical experiments that a decrease in both fractal dimensions $\zeta$ and $ϵ$ leads to an increase in the number of people living with diabetes mellitus.

Keywords: Caputo derivative; Diabetes mellitus model; Fractal-fractional operator; Linear stability analysis; Numerical simulations.

Fig. 1

Diagrammatic flowchart for the diabetes mellitus model

Fig. 2

Simulation results for fractal-fractional diabetes mellitus in the sense of Caputo with varying orders. Other parameters are set as $\kappa =1,\mu =0.13869,\delta =0.06654,\sigma =0.09281,\beta =0.0009,\alpha \gamma =0.88187$. Simulation runs for time $t=80$

Fig. 3

numerical results with $\kappa =1,\beta =0.009$ for different instances of $\zeta$ and $ϵ$. Other parameters are given in Fig. 2 caption

Fig. 4

numerical results with $\kappa =0.02,\beta =0.009$ for different instances of $\zeta$ and $ϵ$. Other parameters are given in Fig. 2 caption

Fig. 5

Numerical results showing the effect of $\kappa =0.50$ for different instances of $\zeta$ and $ϵ$. Other parameters are given in Fig. 2 caption

Fig. 6

The presence of attractors show that the entire population coexist and permanents regardless of time (days) and fractal-fractional orders. Parameters are given in Fig. 2 caption

Fig. 7

The presence of attractors showing the effect of $\beta =0.02(0.02)0.08$. The fractal-fractional parameters are given as $\zeta =0.98$ and $ϵ=0.99$

Fig. 8

Numerical results showing effects of $\beta$ with fixed values of $\zeta =0.98$ and $ϵ=0.99$. Other parameters remain as defined in Fig. 2 caption