Fast strain mapping in abdominal aortic aneurysm wall reveals heterogeneous patterns

Abstract

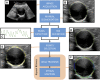
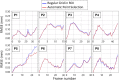
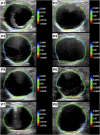
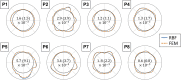
Abdominal aortic aneurysm patients are regularly monitored to assess aneurysm development and risk of rupture. A preventive surgical procedure is recommended when the maximum aortic antero-posterior diameter, periodically assessed on two-dimensional abdominal ultrasound scans, reaches 5.5 mm. Although the maximum diameter criterion has limited ability to predict aneurysm rupture, no clinically relevant tool that could complement the current guidelines has emerged so far. In vivo cyclic strains in the aneurysm wall are related to the wall response to blood pressure pulse, and therefore, they can be linked to wall mechanical properties, which in turn contribute to determining the risk of rupture. This work aimed to enable biomechanical estimations in the aneurysm wall by providing a fast and semi-automatic method to post-process dynamic clinical ultrasound sequences and by mapping the cross-sectional strains on the B-mode image. Specifically, the Sparse Demons algorithm was employed to track the wall motion throughout multiple cardiac cycles. Then, the cyclic strains were mapped by means of radial basis function interpolation and differentiation. We applied our method to two-dimensional sequences from eight patients. The automatic part of the analysis took under 1.5 min per cardiac cycle. The tracking method was validated against simulated ultrasound sequences, and a maximum root mean square error of 0.22 mm was found. The strain was calculated both with our method and with the established finite-element method, and a very good agreement was found, with mean differences of one order of magnitude smaller than the image spatial resolution. Most patients exhibited a strain pattern that suggests interaction with the spine. To conclude, our method is a promising tool for investigating abdominal aortic aneurysm wall biomechanics as it can provide a fast and accurate measurement of the cyclic wall strains from clinical ultrasound sequences.

Keywords: abdominal aortic aneurysm; finite element modeling; radial basis functions; strain imaging; ultrasound B-mode cine-loops; ultrasound elastography; ultrasound simulations; vascular wall strains.

FIGURE 1

Proposed methodology for strain mapping in the AAA wall. (A) 2D US cine-loop sequence acquired from an AAA patient. (B) The AAA inner wall is manually segmented by placing landmark points on the first frame of the sequence. (C) Automatic motion tracking analyzes the evolution of the antero-posterior diameter throughout the sequence to detect the pressure cycle peaks. (D) A region of interest (ROI) is defined based on the manual segmentation of the wall. (E) An automatic point selection algorithm is applied in the region of interest, defining tracking points. (F) For each pressure cycle, the wall motion is tracked, and the strain maps are computed to be displayed as an overlay grid on top of the 2D US sequence.

FIGURE 2

Example of a wall grid used for strain mapping. The grid is obtained by resampling the manually selected contour with N equally spaced points. Each of the N points is projected outward along the normal direction at a distance of 2 mm from the inner wall. The normal direction is obtained by a 90° rotation of the segments connecting the point to the four adjacent grid nodes, as shown by the red arrow. The obtained outer wall is resampled again with N points to guarantee regular grid spacing, keeping the most posterior point fixed. The final grid is obtained by building two intermediate layers by partitioning the segment connecting the inner layer to the outer layer nodes into three segments. Therefore, the connecting segments are not necessarily normal to the vessel wall. N is chosen to guarantee an aspect ratio of the grid elements close to 1.

FIGURE 3

Schematic of a bilinear element with reduced integration. Linear elements approximate the finite-element method solution and are very common as they are computationally efficient and robust to large element distortions, simplifying the meshing problem. They have four nodes (orange dots), and the solution is calculated in the element centroid (blue dot). ξ and η are the directions from which shape functions are defined.

FIGURE 4

Boxplots of the cycle length (left) and of the cyclic antero-posterior diameter variation (right) in the selected cycles for all patients. For each patient, results are presented for the C5-1 probe (red) and X6-1 probe (orange).

FIGURE 5

Examples of original (left) and simulated (right) 2D US frames used for AAA wall tracking validation. The original sequence (Patient 3) was acquired with a C5-1 probe. Both images have a spatial resolution of 0.22 mm × 0.22 mm. The animated simulated sequence is reported in Supplementary Video S1.

FIGURE 6

Per patient evolution of the root mean square error (RMSE) between the imposed ground truth displacement field and the tracking result for two tracking strategies throughout the first cycle of the template sequence. The blue plots are obtained by tracking the wall in the points corresponding to the nodes of the regular grid defined for strain mapping. The red lines are obtained by tracking the points that were automatically selected based on the gradient values.

FIGURE 7

Circumferential strain maps overlaid on the reference peak systolic frame of each patient (C5-1 probe). The color scale is adapted per patient based on the range of the strain in the sequence. Positive strains (blue) indicate circumferential stretch and negative (red) indicate circumferential shortening.

FIGURE 8

Boxplots showing the circumferential strains in the cycle of reference. The wall was divided into four sectors: posterior (top left), anterior (top right), left side (bottom left), and right side (bottom right) in accordance with the transversal 2D US imaging plane. Results are presented for the C5-1 probe (green) and the X6-1 probe (orange).

FIGURE 9

Circumferential strains in all patients and their inter-cycle reproducibility, reported for the C5-1 probe (A) and the X6-1 probe (B). The polar plots depict the circumferential strains in the systolic peaks of each analyzed cycle (in light red) and in the reference cycle (in dark red), averaged over the layers of the output grid. The representation is coherent with 2D US orientation. For each sequence, the number of analyzed cycles is reported inside the polar plot. The strain values (radial coordinate in the plots) range from −0.01 to 0.01. The meaning of negative and positive values is illustrated in the scheme on the left.

FIGURE 10

Superimposition of circumferential (CIRC-red) and radial (RAD-green) strain polar plots in the reference cycle peak systolic frame, averaged over the layers of the output grid. Interpretation of positive and negative values in circumferential (top) and radial (bottom) directions is provided in the schemes on the left.

FIGURE 11

Polar plots assessing the inter-probe reproducibility of strain measures. The circumferential strains in the reference peak systolic frame are depicted for all the patients, averaged over the layers of the output grid, for the C5-1 probe (solid red line) and X6-1 probe (dashed blue line). The strain value (radial coordinate) ranges from −0.01 to 0.01. The polar plots have the same orientation as the 2D US scan (i.e., with the AAA posterior wall on the bottom).

FIGURE 12

Polar plots comparing the finite element (FEM) and radial basis function (RBF) methods for strain validation. The maximum principal strains are displayed for each analyzed sequence with the RBF differentiation method (blue solid line) and with FEM shape functions (orange dotted line). The polar plots are in the same orientation as the 2D US scan, and the strain values range from 0 to 0.25 (radial coordinate). The values are reported for grids with an element size of 1 px and for the frame with the highest absolute difference. The mean absolute difference between the two methods and the standard deviation for each sequence are reported in the center of each polar plot (Mean (standard deviation)).

FIGURE 13

Comparison of the mesh convergence rates in the finite element method (FEM) and the radial basis function (RBF) methods. Convergence of the maximum strain in the maximum principal direction obtained with the RBF differentiation method (left) and the FEM reduced integration method (right).