Sinogram Inpainting with Generative Adversarial Networks and Shape Priors
- PMID: 37368546
- PMCID: PMC10301347
- DOI: 10.3390/tomography9030094
Sinogram Inpainting with Generative Adversarial Networks and Shape Priors
Abstract
X-ray computed tomography is a widely used, non-destructive imaging technique that computes cross-sectional images of an object from a set of X-ray absorption profiles (the so-called sinogram). The computation of the image from the sinogram is an ill-posed inverse problem, which becomes underdetermined when we are only able to collect insufficiently many X-ray measurements. We are here interested in solving X-ray tomography image reconstruction problems where we are unable to scan the object from all directions, but where we have prior information about the object's shape. We thus propose a method that reduces image artefacts due to limited tomographic measurements by inferring missing measurements using shape priors. Our method uses a Generative Adversarial Network that combines limited acquisition data and shape information. While most existing methods focus on evenly spaced missing scanning angles, we propose an approach that infers a substantial number of consecutive missing acquisitions. We show that our method consistently improves image quality compared to images reconstructed using the previous state-of-the-art sinogram-inpainting techniques. In particular, we demonstrate a 7 dB Peak Signal-to-Noise Ratio improvement compared to other methods.
Keywords: Generative Adversarial Network; X-ray computed tomography; computer assisted design data; machine-learning.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
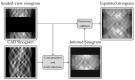

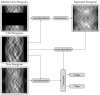






References
-
- du Plessis A., le Roux S.G., Guelpa A. Comparison of medical and industrial X-ray computed tomography for non-destructive testing. Case Stud. Nondestruct. Test. Eval. 2016;6:17–25. doi: 10.1016/j.csndt.2016.07.001. - DOI
-
- Feldkamp L.A., Davis L.C., Kress J.W. Practical Cone-Beam Algorithm. Ford Motor Company; Dearborn, MI, USA: 1984. Technical Report 6.
-
- Biguri A., Dosanjh M., Hancock S., Soleimani M. TIGRE: A MATLAB-GPU toolbox for CBCT image reconstruction. Biomed. Phys. Eng. Express. 2016;2:055010. doi: 10.1088/2057-1976/2/5/055010. - DOI
-
- Candès E.J., Romberg J., Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory. 2006;52:489–509. doi: 10.1109/TIT.2005.862083. - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
Miscellaneous

