Hierarchical Wilson-Cowan Models and Connection Matrices

Abstract

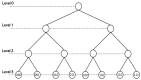
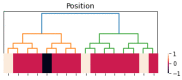
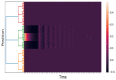
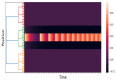
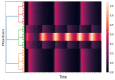
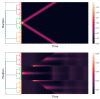
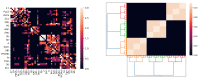
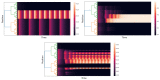
This work aims to study the interplay between the Wilson-Cowan model and connection matrices. These matrices describe cortical neural wiring, while Wilson-Cowan equations provide a dynamical description of neural interaction. We formulate Wilson-Cowan equations on locally compact Abelian groups. We show that the Cauchy problem is well posed. We then select a type of group that allows us to incorporate the experimental information provided by the connection matrices. We argue that the classical Wilson-Cowan model is incompatible with the small-world property. A necessary condition to have this property is that the Wilson-Cowan equations be formulated on a compact group. We propose a p-adic version of the Wilson-Cowan model, a hierarchical version in which the neurons are organized into an infinite rooted tree. We present several numerical simulations showing that the p-adic version matches the predictions of the classical version in relevant experiments. The p-adic version allows the incorporation of the connection matrices into the Wilson-Cowan model. We present several numerical simulations using a neural network model that incorporates a p-adic approximation of the connection matrix of the cat cortex.

Keywords: Wilson–Cowan model; connection matrices; p-adic numbers; small-world networks.

Figure 1

The rooted tree associated with the group ${\mathbb{Z}}_2/2^3{\mathbb{Z}}_2$. The elements of ${\mathbb{Z}}_2/2^3{\mathbb{Z}}_2$ have the form $i=i_0+i_{1}2+i_2{2}^2$,$i_0$, $i_1$, $i_2\in \{0,1\}$. The distance satisfies $-{log}_2{\left|i-j\right|}_2=$ level of the first common ancestor of i, j.

Figure 2

Heat map of function $\varphi \left(x\right)$; see (18). Here, $\varphi \left(0\right)=\varphi \left(1\right)=\varphi \left(7\right)=1$ is white; $\varphi \left(2\right)=-1$ is black; and $\varphi \left(x\right)=0$ is red for $x\ne 0,1,7,2$.

Figure 3

An approximation of $E(x,t)$. We take $Q=0$ and $\delta =5$. The time axis goes from 0 to 100 with a step of $0.05$. The figure shows the response of the network to a brief localized stimulus (the pulse given in (19)). The response is also a pulse. This result is consistent with the numerical results in [2] (Section 2.2.1, Figure 3).

Figure 4

An approximation of $E(x,t)$. We take $Q=0$ and $\delta =100$. The time axis goes from 0 to 200 with a step of $0.05$. The figure shows the response of the network to a maintained stimulus (see (19)). The response is a pulse train. This result is consistent with the numerical results in [2] (Section 2.2.5, Figure 7).

Figure 5

An approximation of $E(x,t)$. We take $Q=-30$ and $\delta =100$. The time axis goes from 0 to 100 with a step of $0.05$. The figure shows the response of the network to a maintained stimulus (see (19) and (20)). The response is a pulse train in space and time. This result is consistent with the numerical results in [2] (Section 2.2.7, Figure 9).

Figure 6

An approximation of ${\tilde{h}}_E(x,t)$ and $E(x,t)$. We take $h_I(x,t)\equiv 0$, $p=3$, and $l=6$; the kernels $w_{AB}$ are as in Simulation 1, and $h_E(x,t)$ is as in (21). The time axis goes from 0 to 60 with a step of $0.05$. The first figure is the stimuli, and the second figure is the response of the network.

Figure 7

An approximation of $h_E(x,t)$ and $E(x,t)$. We take $h_I(x,t)\equiv 0$, $p=3$, and $l=6$; the kernels $w_{AB}$ are as in Simulation 1, and $h_E(x,t)$ is as in (22). The time axis goes from 0 to 60 with a step of $0.05$. The first figure is the stimuli, and the second figure is the response of the network.

Figure 8

The left matrix is the connection matrix of the cat cortex. The right matrix corresponds to a discretization of the kernel $w_{EE}$ used in Simulation 1.

Figure 9

Three p-adic approximations for the connection matrix of the cat cortex. We take $p=2$ and $l=6$. The first approximation uses $r=0$; the second, $r=3$; and the last, $r=5$.

Figure 10

We use $p=2$ and $l=6$, and the time axis goes from 0 to 150 with a step of $0.05$. The left image uses $r=0$; the right one uses $r=3$; and the central one uses $r=5$.