Pulsed stimulated Brillouin microscopy

Abstract

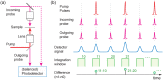
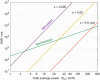
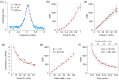
Stimulated Brillouin scattering is an emerging technique for probing the mechanical properties of biological samples. However, the nonlinear process requires high optical intensities to generate sufficient signal-to-noise ratio (SNR). Here, we show that the SNR of stimulated Brillouin scattering can exceed that of spontaneous Brillouin scattering with the same average power levels suitable for biological samples. We verify the theoretical prediction by developing a novel scheme using low duty cycle, nanosecond pulses for the pump and probe. A shot noise-limited SNR over 1000 was measured with a total average power of 10 mW for 2 ms or 50 mW for 200 µs integration on water samples. High-resolution maps of Brillouin frequency shift, linewidth, and gain amplitude from cells in vitro are obtained with a spectral acquisition time of 20 ms. Our results demonstrate the superior SNR of pulsed stimulated Brillouin over spontaneous Brillouin microscopy.

Fig. 1.

Schematic of the interlaced pulse scheme for stimulated Brillouin microscopy. (a) An optical setup with a probe beam and a counterpropagating pump beam. (b) The timing diagram of pump pulses with a duty cycle $\kappa$ and probe pulses with twice the repetition rate. The detector signal of the probe beam going through the sample is digitized and integrated with specified boxcar windows. The difference of the integrated values between each adjacent pair of windows (n0 without pump and n1 with pump) is recorded and plotted as the frequency difference between the pump and probe light is scanned. This produces a Brillouin spectrum.

Fig. 2.

Theoretical plot of $SNR$ per 1 millisecond integration time for different cases based on Eq. (2) for spontaneous Brillouin microscopy and Eq. (4) for stimulated Brillouin microscopy. The pulsed scheme with low duty cycle allows for a higher SNR than spontaneous Brillouin microscopy with low power exposure to samples.

Fig. 3.

Schematic of the microscope system. BE: beam expander, BD: balanced detector, BPF: 780 nm bandpass filter (Δλ=3 nm), BS: beam splitter, CCD: charged coupled device camera, DBC: dichroic beam combiner, EOM: electro-optic modulator, FPBS: fiber polarization beam splitter, Obj: objective lens (60X NA = 1.1), OP: polarization maintaining optical fiber, PBS: polarization beam splitter, PM: polarization maintaining fiber delay, P1 and P2: photodiodes, λ/2: half-wave plate, and λ/4: quarter-wave plate.

Fig. 4.

Experimental data obtained from water. (a) Brillouin gain spectrum obtained with 100 ns pulses. The measured peak SNR at 5.05 GHz is 1280, and the linewidth is 316 MHz. (b) SNR vs. pump peak power at $P_r$ = 50 mW, (c) SNR vs. probe peak power at $P_p$ = 1 W. SNR over 1000 is measured with $⟨P_p⟩$  = 45 mW. (d) Brillouin frequency shift uncertainty ${\sigma }_{fB}$ vs. probe peak power at $P_p$ = 1 W. (e) SNR vs. pulse width at $P_p$ = 1 W and $P_r$ = 50 mW, (f) SNR vs. pulse width $\tau$ at $⟨P_p⟩$  = 10 mW and $P_r$ = 50 mW. With $\kappa$  = 0.01, SNR over 1000 is measured with $⟨P_{tot}⟩$  = 10 mW. Error bars: standard deviations over 100 measurements. The data integration time is 200 µs in (b-e) and 2 ms (f). Circles, experimental data. Red curves, theory (polynomials).

Fig. 5.

Brillouin images of live cells in vitro. (a) Brillouin frequency shift, gain, and linewidth image of a HeLa cancer cell, accompanied with bright-field images (gray) and confocal fluorescent images (indigo: nucleus, red: membrane). Number of pixels: 100 × 240 (H x V) in (a) and 200 × 100 in (b).

Fig. 6.

Time-lapse fluctuations of Brillouin parameters at fixed locations in a sample. The spectral acquisition time is 20 ms. (a) Brillouin frequency shift, (b) Linewidth and amplitude in the extracellular culture medium, (c) Linewidth and amplitude in the nucleolus, and (d) histogram of Brillouin frequency in the nucleolus with a Gaussian fit.