Demonstration of quantum-digital payments

Abstract

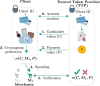
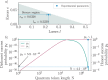
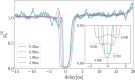
Digital payments have replaced physical banknotes in many aspects of our daily lives. Similarly to banknotes, they should be easy to use, unique, tamper-resistant and untraceable, but additionally withstand digital attackers and data breaches. Current technology substitutes customers' sensitive data by randomized tokens, and secures the payment's uniqueness with a cryptographic function, called a cryptogram. However, computationally powerful attacks violate the security of these functions. Quantum technology comes with the potential to protect even against infinite computational power. Here, we show how quantum light can secure daily digital payments by generating inherently unforgeable quantum cryptograms. We implement the scheme over an urban optical fiber link, and show its robustness to noise and loss-dependent attacks. Unlike previously proposed protocols, our solution does not depend on long-term quantum storage or trusted agents and authenticated channels. It is practical with near-term technology and may herald an era of quantum-enabled security.

Fig. 1. Simplified representation of quantum-digital payments.

As in classical payments, we consider three parties: a Client, a Merchant, and a Bank/Creditcard institute. In contrast to ref. , we do not assume any quantum or classical communication channel to be trusted (i.e., CH 1, CH 2, and CH 3 are insecure), except an initial prior step between the Bank and Client for an account creation. All parties involved apart from the Bank can also act maliciously. During a payment, the Bank sends a set of quantum states to the Client’s device (e.g., phone, computer, etc.), which measures them and transforms them into a quantum-secured payment token—cryptogram—which we display here as a one-time credit card. The Client uses this classical token for paying the Merchant, who then contacts the Bank for payment verification. If the payment is accepted, the bank transfers the money from the Client’s account to the Merchant’s.

Fig. 2. Classical digital payments.

Step 0: The Client sets up an account at the Trusted Token Provider (TTP), providing their secret ID and sensitive credit card information through an authenticated and encrypted channel. Step 1: The Client authenticates with the TTP, and requests a cardholder token C, which the TTP sends through a secure channel. Step 2: The TTP randomly generates a one-time token P and sends it to the Client through a secure channel. Step 3: The Client’s device uses the stored secret token C, the public merchant ID M_i, and the payment token P to compute a cryptogram $\kappa \left(C,M_i,P\right)$. Step 4: The Client spends the cryptogram at the chosen Merchant. Step 5: The Merchant verifies the cryptogram with the TTP, and accepts or rejects the transaction.

Fig. 3. Experimental quantum-digital payments.

a The Trusted Token Provider (TTP) creates entangled photon pairs using a Spontaneous Parametric Down Conversion (SPDC) source. One photon’s polarization is randomly measured by the TTP in either a linear or diagonal basis, creating the classical description $\left(b,\mathcal{B}\right)$, which remotely prepares the quantum token $∣P⟩$ on the second photon. The latter is sent to the Client through a 641 m long optical fiber link, who measures its polarization in a basis m_i = MAC(C, M_i) specified by a Message Authentication Code (MAC) of the Merchant’s ID M_i and the Client’s private token C, and thereby obtains the cryptogram that is ${\kappa }_i\stackrel{m_i}{\leftarrow }∣P⟩$. Classical communication between the TTP, Client and Merchant is used to verify the compatibility of κ, M_i and C with $\left(b,\mathcal{B}\right)$. Red (blue) lines indicate quantum (classical) channels. The arrow numbering indicates the steps from Fig. 2. b Satellite image of the two buildings housing the TTP, Client, and Merchant. A 641 m optical fiber link connects the parties.

Fig. 4. Security for experimental quantum cryptograms.

a The semidefinite programming framework extracts a secure region of operation (turquoise) as a function of errors and losses. Our measured experimental performance (e_m = 0.0328 ± 0.0001; l_m = 0.2239 ± 0.0150) is indicated by the blue dot, and lies within the secure region. Error bars propagate Poisson errors on coincidence counts. b The dishonest success probability p_d (green, upper bound) and honest success probability p_h (red, lower bound) are displayed as a function of the number of quantum states N required to verify one bit of the cryptogram. These are derived using a Chernoff bound argument (see Supplementary Information). As an example, an experimental token containing λ = N = 4.2 × 10⁶ quantum states (vertical blue dashed line) achieves an honest success probability very close to p_h ~ 1 and a dishonest success probability p_d = 5.9 × 10⁻⁴⁵.

Fig. 5. Heralded second-order correlation function.

Data were acquired for 60 mins at a pump power of 35 mW. Coincidences were calculated using four different time windows: 0.33 ns (green), 0.99 ns (blue), 1.98 ns (red), 2.96 ns (violet). From this measurement, we determine $g_h^{\left(2\right)}\left(0\right)=0.03010\left(14\right)$ for the coincidence window used in the implementation of the protocol. Shaded areas represent error-propagated uncertainties due to Poissonian photon statistics.