Toward reproducible models of sequence learning: replication and analysis of a modular spiking network with reward-based learning

Abstract

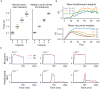
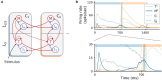
To acquire statistical regularities from the world, the brain must reliably process, and learn from, spatio-temporally structured information. Although an increasing number of computational models have attempted to explain how such sequence learning may be implemented in the neural hardware, many remain limited in functionality or lack biophysical plausibility. If we are to harvest the knowledge within these models and arrive at a deeper mechanistic understanding of sequential processing in cortical circuits, it is critical that the models and their findings are accessible, reproducible, and quantitatively comparable. Here we illustrate the importance of these aspects by providing a thorough investigation of a recently proposed sequence learning model. We re-implement the modular columnar architecture and reward-based learning rule in the open-source NEST simulator, and successfully replicate the main findings of the original study. Building on these, we perform an in-depth analysis of the model's robustness to parameter settings and underlying assumptions, highlighting its strengths and weaknesses. We demonstrate a limitation of the model consisting in the hard-wiring of the sequence order in the connectivity patterns, and suggest possible solutions. Finally, we show that the core functionality of the model is retained under more biologically-plausible constraints.

Keywords: modularity; reproducibility; reward-based learning; sequence learning model; spiking networks.

Figure 1

Sequence learning task and network architecture. (A) A sequence of three intervals (elements) is learned by a network with as many dedicated populations (columns). The individual populations are stimulated sequentially, with a global reward signal given at the beginning and the end of each element. After training, the recurrent and feedforward weights are strengthened, and the sequence is successfully recalled following a cue. The fullness of the colored sections on the right illustrates the duration of the activity (firing rates) above a certain threshold. (B) Each stimulus-specific column is composed of two excitatory, Timers (T) and Messengers (M), and two corresponding inhibitory populations, I_T and I_M. Solid (dashed) arrows represent fixed static (plastic) connections. Cross-columnar inhibition always targets the excitatory population in the corresponding layer (L₅ or L_2/3). (C) Firing rates of the excitatory populations during learning (top three plots) and recall (bottom plot) of four time intervals (500; 1,000; 700; and 1,800ms). Light (dark) colors represent T (M) cells. Dashed light blue curve in top panel inset shows the inhibitory population I_T in L₅. Green (gray) vertical bars show the 25ms reward (trace refractory) period, 25ms after stimulus offset (see inset). (D) Spiking activity of excitatory cells (top) and corresponding ISI distributions (bottom), during recall, for the network in (C). In the raster plot, neurons are sorted by population (T, M) and sequentially by column (see color coding on the right).

Figure 2

Accuracy of recall and evolution of learning. Results shown for a sequence of four intervals of 700ms. (A) Fluctuations in learning and sequence recall. We define recall time as the time at which the rate of the Timer population drops below 10spks/sec. Left: recall times for 30 trials after learning, for one network instance. Right: distribution of the median recall times over 10 network instances, with the median in each network calculated over 30 replay trials. (B) Mean synaptic weights for feedforward (Messenger to Timer in subsequent columns, top) and recurrent (Timer to Timer in the same column, bottom) connections for one network instance. (C) Mean LTP and LTD traces for the recurrent (top) and feedforward (bottom) connections, for learning trials T = 3, T = 15, and T = 35 and one network instance.

Figure 3

Robustness to variation in synaptic weights and learning parameters. The system was trained on a sequence of four elements, each with a duration of 700ms. For the Timer cells, we define relative recall time as the recall time relative to stimulation onset, i.e., the time from the expected onset time (0; 7,00; 1,400; 2,100) in the sequence until the rate drops below a threshold of 10spks/sec. Conversely, absolute recall time is simply the time when the rate drops below threshold (relative to 0). (A) Number of outlier intervals reported during 50 recall trials, as a function of the percentage change of two synaptic weights within a column: excitatory Timer to Messenger, and inhibitory I_T to Messenger. Top row shows the number of outliers, defined as a deviation of ±140 ms from the correct interval relative to expected onset (left), and the number of outliers detected using a modified z-score (threshold >3, right panel) based on the median absolute deviation in column C₄ (see main text). Bottom row shows the respective outliers averaged over all four columns. (B) Deviation of the median recall time from the expected 700ms, as a function of the excitatory and inhibitory synaptic weights onto the Messenger cells in a column (left), and as a function of the cross-columnar (C_i≠C_j) inhibitory synaptic weights within the same layers (right). Top and bottom row as in (A). All data in (A, B) is averaged over 20 network instances. (C) Mean recall time of a four-element sequence of 700ms intervals, over 50 recall trials of a single network instance. Left: baseline network. Center: during each training trial, the learning parameters (see main text) are drawn randomly and independently from a distribution of ±20% around their baseline value. Error bars represent the standard deviation. Right: the set of learning parameters is drawn randomly once for each network instance, with data shown averaged over 10 instances.

Figure 4

Activity of L₅ inhibitory population is critical for accurate learning. (A) Deviation of the median recall time of three intervals of 700ms, as a function of the change in synaptic weights T→I_T relative to baseline (Δw = 0). Gray area (<−25%) marks region where learning is unstable (not all elements can be recalled robustly). Data is averaged over five network instances. (B–D) Characteristic firing rates during recall for values deviations of −25, 0, and 40% relative to baseline. Solid curves represent the excitatory populations as in Figure 1, while dashed curves indicate the respective inhibitory populations I_T in C_i.

Figure 5

Scaling the model requires manual retuning of parameters. (A) Characteristic firing rates during training (top) and recall (bottom) of a sequence composed of three 700ms intervals, in a larger network where each population is composed of N′ = 400 cells. All static weights have been scaled down by $1/\sqrt{N^{\prime }/N}$ (see Methods). Solid curves show Timer (light) and Messenger (dark) cells, dashed curves I_T cells. (B) As in (A), with further manual tuning of specific weights. For details, see Section 4 and Supplementary material.

Figure 6

All-to-all cross-columnar excitation prohibits learning. (A) Extending the original architecture described in Figure 1B, M→T connections exist between all columns C_i→C_j (i≠j) and are subject to the same plasticity. (B) Firing rates of the excitatory populations during learning and recall of four time intervals (each 700 ms). Initially, learning evolves as in Figure 1C, but the activity becomes degenerated and the sequence can not be recalled correctly (lower panels). (C) Evolution of the cross-columnar (from C₂, top panel) and recurrent Timer synaptic weights (bottom panel). The transition to the next sequence cannot be uniquely encoded as the weights to all columns are strengthened. (D) Sequence recall after 100 training trials in a network with a low background noise (50% of the baseline value, 1/2σ_ξ). (E) Sequence recall after 100 training trials in a network with a higher Hebbian activation threshold for the cross-columnar projections $r_{\text{th}}^{\text{ff}}=30\text{spks}/\text{sec}$ (instead of the baseline 20spks/sec).

Figure 7

Alternative wiring with local inhibition and only excitatory cross-columnar projections. (A) Architecture with local inhibition functionally equivalent to Figure 1B. Inhibitory projections are now local to the column, and feedforward inhibition is achieved via cross-columnar excitatory projections onto the I populations. (B) Recall of a sequence composed of two 700ms intervals. Inset (bottom panel) zooms in on the activity at lower rates. As before, color codes for columns. Color shade represents populations in L₅ (light) and L_2/3 (dark), with solid curves denoting excitatory populations. Dashed (dotted) curves represent the inhibitory cells I_T (I_M).