Physics-informed reinforcement learning for motion control of a fish-like swimming robot

Abstract

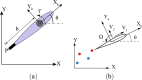
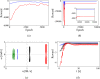
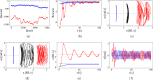
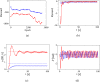
Motion control of fish-like swimming robots presents many challenges due to the unstructured environment and unmodelled governing physics of the fluid-robot interaction. Commonly used low-fidelity control models using simplified formulas for drag and lift forces do not capture key physics that can play an important role in the dynamics of small-sized robots with limited actuation. Deep Reinforcement Learning (DRL) holds considerable promise for motion control of robots with complex dynamics. Reinforcement learning methods require large amounts of training data exploring a large subset of the relevant state space, which can be expensive, time consuming, or unsafe to obtain. Data from simulations can be used in the initial stages of DRL, but in the case of swimming robots, the complexity of fluid-body interactions makes large numbers of simulations infeasible from the perspective of time and computational resources. Surrogate models that capture the primary physics of the system can be a useful starting point for training a DRL agent which is subsequently transferred to train with a higher fidelity simulation. We demonstrate the utility of such physics-informed reinforcement learning to train a policy that can enable velocity and path tracking for a planar swimming (fish-like) rigid Joukowski hydrofoil. This is done through a curriculum where the DRL agent is first trained to track limit cycles in a velocity space for a representative nonholonomic system, and then transferred to train on a small simulation data set of the swimmer. The results show the utility of physics-informed reinforcement learning for the control of fish-like swimming robots.

Figure 1

(a) A Chaplygin sleigh shaped as a Joukowski foil with a no slip constraint at P in the transverse ($Y_b$) direction. The internal reaction wheel is shown by the grey circle. (b) A Joukowski foil with singular distributions of vorticity (red circles corresponding to positive (counterclockwise) vorticity, and blue circles corresponding to negative (clockwise) vorticity) in an otherwise inviscid flow.

Figure 2

(a) (left) A sample serpentine trajectory for the Chaplygin sleigh where the mean converges to a straight line. (right) In the reduced velocity space the trajectory converges to a ‘figure-8’ limit cycle in $(u,\omega )$. (b) A sample trajectory of the simulated swimmer starting from rest when forced by a periodic torque $\tau =Asin\omega t$. The inset figure shows convergence to a limit cycle in the reduced velocity, $(u,\omega )$, space that is similar to the that of the Chaplygin sleigh, indicating similar underlying dynamics. The velocity is scaled into body lengths per second ([BL/s]). The swimmer moves along a serpentine path (in black) with the average path converging to a straight line.

Figure 3

(a) Limit cycles of the surrogate Chaplygin sleigh (red) and the swimmer (blue) for the same periodic forcing, demonstrating convergence to similar limit cycle trajectories in the reduced velocity space. Two sets of limit cycles are shown, one due to applied periodic torque $\tau =sint$ (limit cycles on the left) and the other due to $\tau =1.2sint$ (limit cycle on the right). (b) The vector field of the governing equations for the surrogate Chaplygin sleigh (red) and the swimmer (blue) at the lower velocity. The units shown are for the simulated swimmer, the Chaplygin sleigh states are dimensionless.

Figure 4

(a) A schematic of pre-training to encode the limit cycle features of the reduced velocity space and periodic gaits into the policy output of an actor. (b) A schematic illustration of the application of the modified DPG algorithm to train a policy that can make the surrogate Chaplygin sleigh track a limit cycle and heading angle.

Figure 5

Total reward during epochs of training on the low-speed Chaplygin sleigh surrogate model for (a) the pre-trained actor and (b) an actor without pre-training. The red and blue lines show the reward while learning a policy to track a high speed ($u_t=2.5$) versus a low speed ($u_t=0.8$) respectively. (c) Limit cycles resulting from the policy learned on the surrogate model for target velocities of 0.8, 1.5 and 2.5 (blue, black, and red respectively) as well as the policy before training (green), and (d) The reward function for this policy in each case.

Figure 6

Trajectories on the hydrofoil after training on a low speed surrogate model actor. (a) Reward function during the epochs of training on fluid-hydrofoil simulations and (b) reward while executing the optimal policy tracking velocities and heading angle starting from rest. (c) Trajectories in the reduced velocity space due to the optimal policy of an actor trained on just the surrogate model and (d) produced by the optimal policy by an actor trained on additional fluid-hydrofoil simulation. (e) Velocity tracking by the hydrofoil for two tracking velocities and (f) simultaneously tracking 0° heading angle. Color legend—tracking speed $u_t=0.8$ blue , $u_t=1.5$ black and $u_t=2.5$ red.

Figure 7

Training a high-speed surrogate model actor. (a) Reward function during the epochs of training on fluid-hydrofoil simulations and (b) the reward while executing the optimal policy tracking velocities and heading angle while starting from rest. (c) Velocity tracking by the hydrofoil for two tracking velocities and (d) simultaneously tracking 0° heading angle. Color legend—tracking speed $u_t=0.8$ blue and $u_t=2.5$ red.

Figure 8

RL without surrogate model or curriculum learning. (a) Reward function for epoch training and (b) Reward function executing the optimal policy by a hydrofoil starting from rest. (c) Tracking low (blue) speed and high speed (red) and (d) simultaneously tracking 0° heading angle. For both cases, reward is lower than when trained with a curriculum. This is largely due to higher velocity error, with the swimmer tasked with reaching the low target speed instead coasting to a near-stop.

Figure 9

Pure-pursuit based path tracking for the simulated swimmer on (pa) a straight line and (pb) sinusoidal path and (pc) a circle. The target velocities for the case of the straight line, sinusoidal path and circle are shown by the dashed lines in (va), (vb) and (vc) respectively. The torques generated to track the straight line, sinusoidal path and circle are shown in (Ta), (Tb) and (Tc), respectively.