Growth modeling approach with the Verhulst coexistence dynamic properties for regulation purposes

Abstract

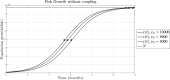
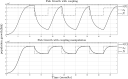
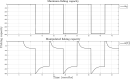
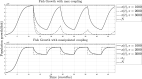
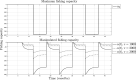
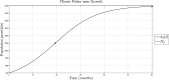
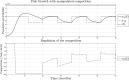
For this research, the properties of the logistic growth model for independent and coexisting species were used to set definitions for the possible regulation of one or two growth variables through their coupling parameters. The present analysis is done for the single-species Verhulst model without coupling, the single-species Verhulst model coupled with an exogenous signal, and the two-species Verhulst coexistence growth model which represents six different ecological regimes of interaction. The models' parameters, such as the intrinsic growth rate and the coupling, are defined. Finally, the control results are expressed as lemmas for regulation, and they are shown using a simulation example of a fish population growing independent of human interaction (no harvesting, no fishing) and the simulation of the regulation of said population when the coupling of fish and humans is involved (harvesting, fishing).

Keywords: Coexistence; Coupling; Dynamic; Growth; Logistic; Regulation.

Fig. 1

Simulation of the Verhulst model for fish growth with different initial conditions when there is no harvest ($\alpha =0$). For $x_0=1000$, the inflection point is reached at $t_{\mathit{inf}}=5.4$, represented by the square, and its final value at $t^{\ast }=11.2$, represented by the circle; for $x_0=800$, $x_{\mathit{ip}}$ is reached at $t_{\mathit{inf}}=5.6$ and $x^{\ast }$ at $t^{\ast }=11.4$; and for $x_0=6000$, $t_{\mathit{inf}}=6$ and $t^{\ast }=11.8$

Fig. 2

Simulation of the coupled Verhulst model for fish growth population. TOP: Population growth with maximum coupling parameters and individuals (${\alpha }_0=-N/v$). BOT: Population growth with the control algorithm ($\alpha (t)$)

Fig. 3

Simulation of the fishing capacity. TOP: Maximum coupling parameters and fishermen ($\alpha =-N/v$ and $v=1000$). BOT: Control algorithm ($\alpha (t)$)

Fig. 4

Simulation of the fish growth with coupling signal. TOP: Fish growth with Maximum coupling parameters (${\alpha }_0=-N/v$ and $v=1000$). BOT: Fish growth using regulation Lemma 4 ($\alpha (t)$) for $v=1000$, $v=2000$, and $v=3000$

Fig. 5

Simulation of the fishing capacity. TOP: Maximum coupling parameters and fishermen ($\alpha =-N/v$ and $v=1000$). BOT: Manipulated coupling parameter ($\alpha (t)$) for $v=1000$, $v=2000$ and $v=3000$

Fig. 6

Simulation of the fishermen’s independent growth, $x_2(t)$, with parameters from Table 4

Fig. 7

Simulation of a fish population coupled with a fisherman population. TOP: Growth of fish population with controlled fishing capacity (continuous line). BOT: Manipulation of the fishing capacity ${\alpha }_1(t)$ (dashed line)