Large-deviations of disease spreading dynamics with vaccination

Abstract

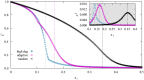
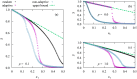
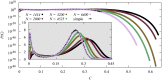
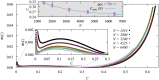
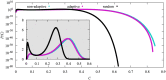
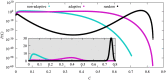
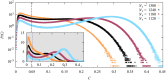
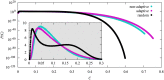
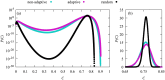
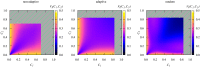
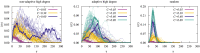
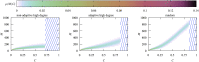
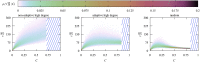
We numerically simulated the spread of disease for a Susceptible-Infected-Recovered (SIR) model on contact networks drawn from a small-world ensemble. We investigated the impact of two types of vaccination strategies, namely random vaccination and high-degree heuristics, on the probability density function (pdf) of the cumulative number C of infected people over a large range of its support. To obtain the pdf even in the range of probabilities as small as 10-80, we applied a large-deviation approach, in particular the 1/t Wang-Landau algorithm. To study the size-dependence of the pdfs within the framework of large-deviation theory, we analyzed the empirical rate function. To find out how typical as well as extreme mild or extreme severe infection courses arise, we investigated the structures of the time series conditioned to the observed values of C.

Fig 1. Average cumulative fraction C¯ of infected nodes for a typical network of N = 3200 nodes for different fractions n_v of vaccinated nodes and the three applied vaccination strategies.

The inset shows the variance σ²(C). The data is obtained by averaging over 10000 samples per point and error bars are not shown as they are smaller than symbol size. The dashed lines indicate the positions of the peaks of the variance, respectively.

Fig 2. Sum S of relatives sizes of the connected components that contain the initial infections, shown as function of n_v.

Results are for a network of size N = 3200, for the different vaccination strategies. Panels (a), (b) and (c) contain the results for different rewiring probabilities p ∈ {0, 0.1, 1}. Each data point was averaged over 20000 samples. Error bars are smaller than the symbol size. We also include an upper bound for the cluster size, which is the fraction of the network that was not yet vaccinated.

Fig 3. Probability density of the cumulative number C of infections for different system sizes N at their critical vaccination doses nvc with the random vaccination strategy as measured by the large-deviation algorithm.

It also includes simple sampling data for the largest system size. Linear scale in the inset.

Fig 4. Rate functions Φ(C) for the random vaccination heuristics for different system sizes N at their respective critical vaccination.

The gray inset shows the position of the minimum of the rate function as a function of N as well as the fit fit-exp with a = 0.142(5), b = 0.00044(4) and $C_{\text{min}}^{\infty }=0.248\left(3\right)$. The other inset shows a zoom for better visibility.

Fig 5. Probability density functions of the cumulative fraction C of infections for N = 3200 for the different vaccination heuristics at their respective critical point.

For the adaptive high-degree heuristics that corresponds to N_v = 530, for the non-adaptive one to N_v = 424, and for the random heuristics to N_v = 1133. Linear scale in the inset.

Fig 6. Probability density functions of the cumulative fraction C of infections for N = 3200 and N_v = 530 for the different vaccination strategies.

Linear scale in inset.

Fig 7. Probability density functions of the cumulative fraction C of infections for the random heuristics, N = 3200, and for different number N_v of vaccinated nodes.

The histograms were measured via simple sampling using 8000000 samples each. Linear scale in the inset. The dashed line indicates the position of the maximum that we aimed for.

Fig 8. Probability density functions of the cumulative fraction C of infected nodes for N = 3200 for the different vaccination strategies.

The non-adaptive high-degree heuristics used N_v = 530, the adaptive one used N_v = 670 and the random heuristics used N_v = 1240. Linear scale in inset.

Fig 9. Probability density functions of the cumulative fraction C of infections for N = 3200 for the different vaccination strategies.

The non-adaptive high-degree heuristics used N_v = 315, the adaptive one used N_v = 305 and the random heuristics used N_v = 530. On the left we show the data in logarithmic scale and on the right the range C ∈ [0.65, 0.85] in linear scale.

Fig 10. Color-coded disparity V_i(C₁, C₂) of the i(τ) time series for N = 3200, N_v = 530.

On the left we show the results for the non-adaptive high-degree vaccination, in the middle the results for the adaptive high-degree vaccination and on the right the results for the random vaccination. The time series are binned with their corresponding value of C and for each bin 1500 randomly drawn time series are used for the calculation of the disparity V_i(C₁, C₂). For the shaded area no time-series exist as it was outside of the interval used for WL.

Fig 11. Infection time series i(τ) for different values of C.

These time series were created during the entropic sampling with a Network of size N = 3200 and a vaccination doses of N_v = 530. On the left we show the results for the non-adaptive high-degree heuristics, in the middle for the adaptive high-degree heuristics and on the right for the random heuristics. For each value of C we plot 30 time series. We also included one arbitrary time series for each C value that we highlighted for clarity.

Fig 12. Color-coded conditional densities ρ(M|C) for a network of N = 3200 nodes and N_v = 530 vaccination doses for the three analyzed vaccination strategies.

The blue stripes indicate the C range that was outside of the Wang-Landau interval.

Fig 13. Conditional density ρ(τ1090|C) that shows the probability of τ1090 for any given value of C for N = 3200 and N_v = 530 for the different vaccination strategies.

The blue stripes indicate the C range that was outside of the Wang-Landau interval.