Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2023 Jun 15;9(6):e17190.
doi: 10.1016/j.heliyon.2023.e17190. eCollection 2023 Jun.

Orthopseudorings and congruences on distributive lattice with dual weak complementation

Eman Ghareeb Rezk  1   2
Affiliations
Review

Orthopseudorings and congruences on distributive lattice with dual weak complementation

Eman Ghareeb Rezk. Heliyon. .

Abstract

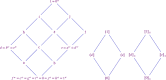
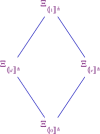
In this article, the concept of weak annulet is defined on the distributive lattice with dual weak complementation (DDWCL). Properties of weak annulets are proved. The relationship between orthopseudoring and ortho-lattice of all weak annulets of DDWCL is demonstrated. Congruence relations, with respect to weak annulets on DDWCL (W-congruences), are established. The double-face algebraic structure of all weak annulets and all W-congruence is investigated.

Keywords: 06B10; 06C15; 06D05; 06E20; 06E75; Congruence relation; Distributive lattice; Dual weakly complemented lattice; Ortho-lattice; Orthopseudoring.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Figures

Figure 1
Figure 1
Graphs of the DDWCL L, ortho-lattice of weak annulets Λ(L) and ortho-lattice of Glivenko congruence classes L/≑.
Figure 2
Figure 2
WCon⋔¯(L) is the ortho-lattice of W-congruence relations on the lattice L.
Figure 3
Figure 3
Graphs of the weakly normal lattice K, Boolean algebra of weak annulets Λ(K) and Boolean algebra of Glivenko congruence classes K/≑.
Figure 4
Figure 4
WCon⋔¯(K) is the Boolean algebra of W-congruence relations on the lattice K.
See this image and copyright information in PMC

References

    1. Chajda Ivan. Pseudosemirings induced by ortholattices. Czechoslov. Math. J. 1996;46:405–411.
    1. Cornish William H. Annulets and δ-ideals in distributive lattices. J. Aust. Math. Soc. 1973;15:70–77.
    1. Gretzer Geoge A. Springer; Basel: 2011. Lattice Theory: Foundation.
    1. Kwuida Leonard. TU Dresden, Shaker Verlag; 2004. Dicomplemented Lattices: A Contextual Generalization of Boolean Algebras. Dissertation.
    1. Rafi N., Bandaru RaviKumar, Srujana M. N-prime spectrum of stone almost distributive lattices. Discus. Math., Gen. Algebra Appl. 2021;41(2):299–320.

LinkOut - more resources