Generalized Linear Models to Forecast Malaria Incidence in Three Endemic Regions of Senegal

Abstract

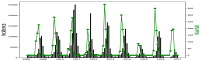
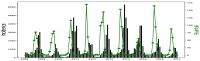
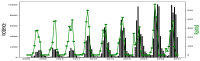
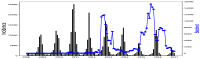
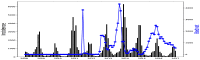
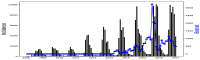
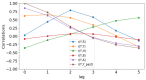
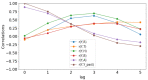
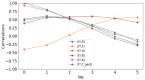
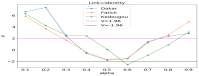
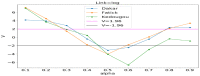
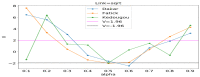
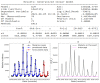
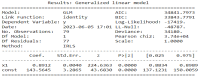
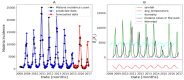
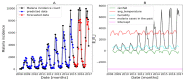
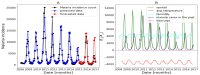
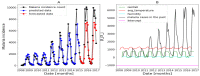
Affecting millions of individuals yearly, malaria is one of the most dangerous and deadly tropical diseases. It is a major global public health problem, with an alarming spread of parasite transmitted by mosquito (Anophele). Various studies have emerged that construct a mathematical and statistical model for malaria incidence forecasting. In this study, we formulate a generalized linear model based on Poisson and negative binomial regression models for forecasting malaria incidence, taking into account climatic variables (such as the monthly rainfall, average temperature, relative humidity), other predictor variables (the insecticide-treated bed-nets (ITNs) distribution and Artemisinin-based combination therapy (ACT)) and the history of malaria incidence in Dakar, Fatick and Kedougou, three different endemic regions of Senegal. A forecasting algorithm is developed by taking the meteorological explanatory variable Xj at time t-𝓁j, where t is the observation time and 𝓁j is the lag in Xj that maximizes its correlation with the malaria incidence. We saturated the rainfall in order to reduce over-forecasting. The results of this study show that the Poisson regression model is more adequate than the negative binomial regression model to forecast accurately the malaria incidence taking into account some explanatory variables. The application of the saturation where the over-forecasting was observed noticeably increases the quality of the forecasts.

Keywords: epidemiological data; forecasting; generalized linear models; meteorological data; parameters estimation.

Figure 1

Location of Dakar, Fatick, and Kedougou in Senegal. The choice of these three regions is motivated by data availability (notably the presence of villages where longitudinal studies have been conducted), but also by geographical differences: influence of the ocean in the Dakar peninsula, tropical climate in Kedougou, and savanna landscape in Fatick. These fundamental geographical differences allow us to test the applicability of GLMs under drastically different evolutions of the climate variables.

Figure 2

Malaria (falciparum malaria incidence count per month, black) and rainfall (mm per month, green) in Dakar, 2008–2016.

Figure 3

Malaria (falciparum malaria incidence count per month, black) and rainfall (mm per month, green) in Fatick, 2008–2016.

Figure 4

Malaria (falciparum malaria incidence count per month, black) and rainfall (mm per month, green) in Kedougou, 2008–2016.

Figure 5

Malaria (falciparum malaria incidence count per month, black) and Bed-net distributed (the number of insecticide treated bed-nets distributed per month, blue) in Dakar, 2008–2016.

Figure 6

Malaria (falciparum malaria incidence count per month, black) and Bed-net distributed (the number of insecticide treated bed-nets distributed per month, blue) in Fatick, 2008–2016.

Figure 7

Malaria (falciparum malaria incidence count per month, black) and Bed-net distributed (the number of insecticide treated bed-nets distributed per month, blue) in Kedougou, 2008–2016.

Figure 8

Correlation plots for Dakar.

Figure 9

Correlation plots for Fatick.

Figure 10

Correlation plots for Kedougou.

Figure 11

V vs. $\alpha$ between Poisson and NB distributions. Estimating $\alpha$ in each region by the ordinary least squares (OLS) method gives 0.109, 0.222 and 0.282, respectively, in Dakar, Fatick, and Kedougou.

Figure 12

V vs. $\alpha$ between Poisson and NB distributions. Estimating $\alpha$ in each region by the ordinary least squares (OLS) method gives 0.142, 0.202 and 0.412, respectively, in Dakar, Fatick, and Kedougou.

Figure 13

V vs. $\alpha$ between Poisson and NB distributions. Estimating $\alpha$ in each region by the ordinary least squares (OLS) method gives 0.119, 0.214 and 0.318, respectively, in Dakar, Fatick, and Kedougou.

Figure 14

Statistical (in top) and forecasting (in bottom) results in Dakar. Malaria incidence means the falciparum malaria incidence count per month. The train/test accuracy measures are RMSE: 3886.43 /2367.55, MASE: 0.95/1.06, MARE: 0.85/1.59, and $R_{\mathrm{COR}}^2$: 0.51/0.54. We present the forecast results (noted by A) and the curves of ${\beta }_j{X}_j$ (noted by B).

Figure 15

Statistical (in top) and forecasting (in bottom) results in Fatick. Malaria incidence means the falciparum malaria incidence count per month. The train/test accuracy measures are RMSE: 916.35/408.29, MASE: 0.96/1.11, MARE: 0.76/0.75, and $R_{\mathrm{COR}}^2$: 0.55/0.5. We present the forecast results (noted by A) and the curves of ${\beta }_j{X}_j$ (noted by B).

Figure 15

Statistical (in top) and forecasting (in bottom) results in Fatick. Malaria incidence means the falciparum malaria incidence count per month. The train/test accuracy measures are RMSE: 916.35/408.29, MASE: 0.96/1.11, MARE: 0.76/0.75, and $R_{\mathrm{COR}}^2$: 0.55/0.5. We present the forecast results (noted by A) and the curves of ${\beta }_j{X}_j$ (noted by B).

Figure 16

Statistical (in top) and forecasting (in bottom) results in Kedougou. Malaria incidence means the falciparum malaria incidence count per month. The train/test accuracy measures are RMSE: 1250.53/2523.74, MASE: 1.02/0.93, MARE: 1.06/0.61, and $R_{\mathrm{COR}}^2$: 0.61/0.59. We present the forecast results (noted by A) and the curves of ${\beta }_j{X}_j$ (noted by B).

Figure 17

Forecasting results in Dakar, no saturation applied. Malaria incidence means the falciparum malaria incidence count per month. We present the forecast results (noted by A) and the curves of ${\beta }_j{X}_j$ (noted by B).

Figure 18

Forecasting results in Fatick: no saturation applied. Malaria incidence means the falciparum malaria incidence count per month. We present the forecast results (noted by A) and the curves of ${\beta }_j{X}_j$ (noted by B).

Figure 19

Forecasting results in Kedougou: no saturation applied. Malaria incidence means the falciparum malaria incidence count per month. We present the forecast results (noted by A) and the curves of ${\beta }_j{X}_j$ (noted by B).

Figure 20

Forecasting results of the saturation in Dakar. Malaria incidence means the falciparum malaria incidence count per month. We present the forecast results (noted by A) and the curves of ${\beta }_j{X}_j$ (noted by B).

Figure 21

Forecasting results of the saturation in Kedougou. Malaria incidence means the falciparum malaria incidence count per month. We present the forecast results (noted by A) and the curves of ${\beta }_j{X}_j$ (noted by B).