Coexistence of Bloch and Parametric Mechanisms of High-Frequency Gain in Doped Superlattices

Abstract

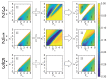
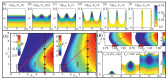
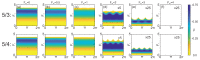
The detailed theoretical study of high-frequency signal gain, when a probe microwave signal is comparable to the AC pump electric field in a semiconductor superlattice, is presented. We identified conditions under which a doped superlattice biased by both DC and AC fields can generate or amplify high-frequency radiation composed of harmonics, half-harmonics, and fractional harmonics. Physical mechanisms behind the effects are discussed. It is revealed that in a general case, the amplification mechanism in superlattices is determined by the coexistence of both the phase-independent Bloch and phase-dependent parametric gain mechanisms. The interplay and contribution of these gain mechanisms can be adjusted by the sweeping AC pump strength and leveraging a proper phase between the pump and strong probe electric fields. Notably, a transition from the Bloch gain to the parametric gain, often naturally occurring as the amplitude of the amplified signal field grows, can facilitate an effective method of fractional harmonic generation in DC-AC-driven superlattices. The study also uncovers that the pure parametric generation of the fractional harmonics can be initiated via their ignition by switching the DC pump electric field. The findings open a promising avenue for the advancement of new miniature GHz-THz frequency generators, amplifiers, and dividers operating at room temperature.

Keywords: amplification; frequency dividers; large signal; microwaves; sub-harmonic; superlattice; terahertz.

Figure 1

Dependencies of the small-signal mobilities (left—incoherent, centre—coherent, right—total) on the applied DC and AC pump field strengths for $3/2{\omega }_0$, $1/2{\omega }_0$, and $5/3{\omega }_0$ frequencies, calculated according to Equations (8) and (9). The coherent mobilities are calculated at the proper optimal values of the phase, and all mobilities are scaled to the Drude mobility ${\mu }_0$. The colours represent the negative values of the mobility components, displaying conditions for the gain associated with the corresponding mobility type. Blank areas mean positive or zero mobility values, thus displaying conditions when the generation is not possible within the small-signal approximation. Solid red lines outline the boundaries of the incoherent gain locus. Both the mathematical model and graphs clearly demonstrate that the incoherent component of the mobility is frequency independent, thus the differences in the total mobility depend only on differences in the coherent component. The total gain diagram of $3/2{\omega }_0$, which is representative for the generation of harmonics and half-harmonics, results in two separated generation areas, the upper left (II) being purely coherent and the bottom right (I) being a mixture of coherent and incoherent components. The case of $1/2{\omega }_0$ is interesting because a specific behaviour of the corresponding coherent component results in the total mobility being in a single area. The physical consequences of such dependence are discussed in Section 3.3. The case of $5/3{\omega }_0$ is typical for the generation of various fractional harmonics: the coherent component vanishes, thus the generation is caused solely by the incoherent gain only. These diagrams of the small-signal gain at characteristic frequencies provide a basis for our further detailed analysis of the large-signal amplification and generation.

Figure 2

Exemplary regions of the large-signal gain ($\overline{P}<0$) shown in the plane of normalized signal amplitude $F_1$ and relative phase $\varphi$ for several characteristic frequency ratios and fixed pump electric field components: (A) ${\omega }_1/{\omega }_0=2$, $F_{\mathrm{dc}}=0$, and $F_{\mathrm{ac}}=5$. The generation process is characterized by a positive gain both for small and large signals when the phase values are close to two green dots, marking the optimal phases ${\varphi }_{\mathrm{opt}}=\pi /2$ and $3\pi /2$. (B) ${\omega }_1/{\omega }_0=5/3$, $F_{\mathrm{dc}}=0$, and $F_{\mathrm{ac}}=5$. Large signal gain arises around the optimal phases (red dots, Equation (5)) only if the probe electric field strength exceeds a threshold. So-called amplification islands are formed. (C) ${\omega }_1/{\omega }_0=7/5$, $F_{\mathrm{dc}}=1$, and $F_{\mathrm{ac}}=10$. The probe electric field requires to overcome a large threshold to achieve gain. By comparing subplots (B) and (C) one can note the difference in the optimal phases and their periodicity. Everywhere the colour palette is used to indicate the power $\overline{P}=P/P_0$ that can be generated within the region of the gain at every given set ($\varphi$, $F_1$). Areas left blank, indicate no gain ($P>0$). Green arrows depict the way the signal can increase through the gain regions. Thin red arrows sketch how an additional ignition mechanism can bring the system into the large-signal gain regime.

Figure 3

The pure parametric generation of half-harmonics and pure parametric amplification of fractional harmonics (large-signal amplification islands). Blank areas denote regions where generation is absent, while colours represent the power $\overline{P}$ value according to Equation (6). The red lines show the incoherent generation boundary of the small-signal model. (A) Maximum generation power dependency on the applied pump electric field (DC and AC) for $3/2{\omega }_0$. The black dashed line and red points, chosen from the type II biasing conditions, show the pump field strengths used to represent the signal vs. phase diagrams in the top inset (a–c)). Top inset (a–c): The signal field dependencies on the relative phase for the pump field strengths $F_{\mathrm{dc}}=0.5$ and $F_{\mathrm{ac}}=$ 2:1:4. We underline that the pure parametric generation at the 3/2-harmonic requires overcoming a significant threshold in AC pump strength ($F_{\mathrm{ac}}\gtrsim 2$). (B): Maximum generation power dependencies on the applied pump electric field (DC and AC) for $5/3{\omega }_0$. The black dashed line and red points show the pump field strengths selected to depict the diagrams in the right inset (d–f). Inset (d–f): Probe electric field dependencies on the relative phase presented for the following pump parameters: $F_{\mathrm{dc}}=0.5$ and $F_{\mathrm{ac}}=$ 4:0.5:5. Note the formation of the large-signal amplification islands with well-defined lower and upper boundaries in the strength of the probe electric field.

Figure 4

Coexistence of the parametric and Bloch gain mechanisms in the $1/2—$harmonic generation. (A) Maximum power $\overline{P}$ (colour, left plot) and the maximum probe field strength (colour, right plot) generated at the optimal phase values. Red thick line marks the boundary of the small-signal incoherent gain (${\mu }_{\mathrm{inc}}<0$, cf. Figure 1). Within the area below this line (region I), the incoherent and coherent gain mechanisms coexist and can compete. Six red dots on the vertical dashed line indicate the fixed pump electric field strengths ($F_{\mathrm{dc}}=4,F_{\mathrm{ac}}=$ 0:4) used to separately depict regions of the large-signal gain ($P<0$, colour) in the plane signal vs. phase. These six diagrams, located in the upper long panel and marked from (a) to (f), clearly expose the transition from completely phase-independent Bloch gain (diagram (a)) to strictly parametric generation (diagram (f)). (B) The upper half presents a zoomed-in view of the generation region framed in Figure 4A. This is located near the critical electric field $F_{\mathrm{dc}}=1$ and at the small AC pump electric field strengths $F_{\mathrm{ac}}<1$. Three black dots, corresponding to $F_{\mathrm{ac}}={10}^{-3}$ and $F_{\mathrm{dc}}$ only slightly below and above the critical electric field, indicate the pump parameters chosen to depict the evolution of the large-signal generation regimes in three diagrams in the bottom half. These diagrams expose the interesting peculiarities of the transition from the pure parametric to dominantly Bloch generation at extremely low levels of the AC pump field.

Figure 5

Transformation of the phase-independent Bloch gain to predominantly parametric gain in the hybrid process of fractional frequency generation. Gain diagrams, showing the dependencies of the probe electric field on the relative phase, are depicted for different pump conditions ($F_{\mathrm{dc}}=4$ and $F_{\mathrm{ac}}=$ 0:4, inset of Figure 4) for the fractional $5/3{\omega }_0$ (upper row) and $5/4{\omega }_0$ (bottom row) frequencies. Colours show the negative values of $\overline{P}$ calculated according to Equation (6), and blank areas indicate that $\overline{P}>0$ where no generation is possible. For a relatively small AC pump field $(F_{\mathrm{ac}}<2)$ the domination of the Bloch gain is expressed in the absence of phase dependency of the probe electric field. However, as the AC pump strength increases, phase-dependent amplification appears, suggesting the formation of large-signal amplification islands. Within these islands, the hybrid gain process exhibits a strong parametric component. Note the absence of generation when the AC pump field exceeds $F_{\mathrm{ac}}=4$ and no Bloch gain exists.

Figure 6

(A) Generated probe electric field profile dependency on the applied pump electric field (DC and AC) for $5/3{\omega }_0$, illustrating the ignition into the amplification island process via switching the DC pump electric field. The orange arrow represents the state switch from “on” $(F_{\mathrm{dc}},F_{\mathrm{ac}})=(4.7,4)$ to “off” $(F_{\mathrm{dc}},F_{\mathrm{ac}})=(0,4)$. Such a change of state allows the pure parametric generation to be reached in amplification islands from a negligibly small probe electric field without applying external AC ignition. (B): Dependence of the probe electric field $F_1$ on the relative phase, corresponding to the states given in Figure 6A (the bottom subplot—“on state” $F_{\mathrm{dc}}=4.7$; the upper subplot—“off state” $F_{\mathrm{dc}}=0$). Blank areas depict conditions where the generation or amplification is not possible. Green arrows represent amplification occurring inside the superlattice, while the dotted orange arrows represent the state change due to switching (cf. Figure 6A).