Self-Sustained Oscillation of Electrothermally Responsive Liquid Crystal Elastomer Film in Steady-State Circuits

Abstract

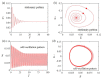
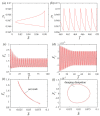
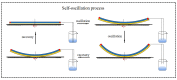
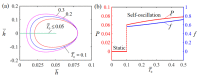
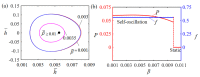
Self-excited oscillations have the advantages of absorbing energy from a stable environment and Self-control; therefore, Self-excited motion patterns have broader applications in micro devices, autonomous robots, sensors and energy-generating devices. In this paper, a Self-sustained curling liquid crystal elastomer (LCE) film-mass system is proposed on the basis of electrothermally responsive materials, which can realize Self-oscillation under a steady-state current. Based on the contact model and dynamic LCE model, a nonlinear dynamics model of LCE film in steady-state circuits is developed and numerical calculations are carried out using the Runge-Kutta method. Through numerical calculations, it is demonstrated that LCE film-mass systems have two motion patterns in steady-state circuits: namely, a Self-oscillation pattern and a stationary pattern. Self-sustained curling of LCE film originates from the fact that the energy absorbed by the system exceeds the energy dissipated due to the damping effect. In addition, the critical conditions for triggering Self-oscillation and the effects of several key dimensionless system parameters on the amplitude and period of Self-oscillation are investigated in detail. Calculation results show that the height of electrolyte solution, gravitational acceleration, elastic modulus of LCE film, limit temperature, curvature coefficient, thermal shrinkage coefficient and damping factor all have a modulating effect on the amplitude and period of Self-oscillation. This research may deepen the understanding of Self-excited oscillation, with promising applications in energy harvesting, power generation, monitoring, soft robotics, medical devices, and micro and nano devices.

Keywords: Self-excited motion; Self-oscillation; dynamic boundary problem; electrothermally responsive; liquid crystal elastomers.

Figure 1

(a) Schematic diagram for the dynamics of a Self-sustained curling LCE film-mass system in a steady-state circuit. (b) Force analysis for the mass block at the end of the LCE film, which is subjected to mass gravity $mg$, damping force $F_f$ and elastic force $F_L$ provided by the LCE film. (c) Enlarged cross-sectional view of the LCE film, showing the electrothermally driven strain distribution in the LCE film, where the upper layer is the LCE film and the lower layer is the insulation layer. (d) Force analysis for the non-contact part of the system with the table, which is subjected to elastic force $F_L$, cross-sectional shear force and bending moment provided by the contact part. In steady-state circuits, the LCE film can curl periodically in a Self-oscillation motion.

Figure 2

(a,b) Plots showing the time course and phase trajectory plots of the steady-state orientation diagram of the LCE membrane-mass system under the conditions of parameters $\overline{H}=0.08$, $\overline{g}=1.2$, $\overline{E}=2.5$, $\overline{A}=0.40$, $\overline{\alpha }=0.35$, $\overline{\dot{h}}=0$, $\overline{\beta }=0.001$ and ${\overline{T}}_0=0.05$. (c,d) Time course and phase trajectory plots of the Self-oscillation pattern of the LCE thin film-mass system under the conditions of parameters $\overline{H}=0.08$, $\overline{g}=1.2$, $\overline{E}=2.5$, $\overline{A}=0.40$, $\overline{\alpha }=0.35$, $\overline{\dot{h}}=0$, $\overline{\beta }=0.001$ and ${\overline{T}}_0=0.1$. There are two modes of motion of the LCE thin film-mass system under steady-state circuits: fixed pattern and Self-oscillation pattern.

Figure 3

(a) Time dependence of electrothermally driven strain in LCE film; (b) displacement dependence of electrothermally driven strain in LCE film; (c) time dependence of the elastic force; (d) time dependence of the damping force; (e) displacement dependence of the elastic force; (f) displacement dependence of the damping force.

Figure 4

Figure 4 shows the Self-excited oscillation of an LCE film-mass system in a steady-state circuit.

Figure 5

Effect of dimensionless height on the Self-sustained curling LCE film-mass system, with $\overline{g}=1.2$, $\overline{E}=2.5$, $\overline{A}=0.40$, $\overline{\alpha }=0.35$, $\overline{\dot{h}}=0$, $\overline{\beta }=0.001$ and ${\overline{T}}_0=0.1$. (a) Limit cycles; (b) amplitude and frequency.

Figure 6

Effect of dimensionless gravitational acceleration on the Self-sustained curling LCE film-mass system with $\overline{H}=0.08$, $\overline{E}=2.5$, $\overline{A}=0.40$, $\overline{\alpha }=0.35$, $\overline{\dot{h}}=0$, $\overline{\beta }=0.001$ and ${\overline{T}}_0=0.1$. (a) Limit cycles; (b) amplitude and frequency.

Figure 7

Effect of dimensionless elastic modulus on a Self-sustained curling LCE film-mass system with $\overline{H}=0.08$, $\overline{g}=1.2$, $\overline{A}=0.40$, $\overline{\alpha }=0.35$, $\overline{\dot{h}}=0$, $\overline{\beta }=0.001$ and ${\overline{T}}_0=0.1$. (a) Limit cycles; (b) amplitude and frequency.

Figure 8

Effect of dimensionless limit temperature on the Self-sustained curling LCE film-mass system with $\overline{H}=0.08$, $\overline{g}=1.2$, $\overline{E}=2.5$, $\overline{A}=0.40$, $\overline{\alpha }=0.35$, $\overline{\dot{h}}=0$ and $\overline{\beta }=0.001$. (a) Limit cycles; (b) amplitude and frequency.

Figure 9

Effect of dimensionless curvature coefficient on the Self-sustained curling LCE film-mass system with $\overline{H}=0.08$, $\overline{g}=1.2$, $\overline{E}=2.5$, $\overline{\alpha }=0.35$, $\overline{\dot{h}}=0$, $\overline{\beta }=0.001$ and ${\overline{T}}_0=0.1$. (a) Limit cycles; (b) amplitude and frequency.

Figure 10

Effect of dimensionless thermal shrinkage coefficient on the Self-sustained curling LCE film-mass system with $\overline{H}=0.08$, $\overline{g}=1.2$, $\overline{E}=2.5$, $\overline{A}=0.40$, $\overline{\dot{h}}=0$, $\overline{\beta }=0.001$ and ${\overline{T}}_0=0.1$. (a) Limit cycles; (b) amplitude and frequency.

Figure 11

Effect of dimensionless damping factor on the Self-sustained curling LCE film-mass system with $\overline{H}=0.08$, $\overline{g}=1.2$, $\overline{E}=2.5$, $\overline{A}=0.40$, $\overline{\alpha }=0.35$, $\overline{\dot{h}}=0$ and ${\overline{T}}_0=0.1$. (a) Limit cycles; (b) amplitude and frequency.