A nonlinear relapse model with disaggregated contact rates: Analysis of a forward-backward bifurcation

Abstract

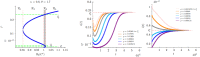
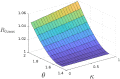
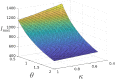
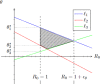
Throughout the progress of epidemic scenarios, individuals in different health classes are expected to have different average daily contact behavior. This contact heterogeneity has been studied in recent adaptive models and allows us to capture the inherent differences across health statuses better. Diseases with reinfection bring out more complex scenarios and offer an important application to consider contact disaggregation. Therefore, we developed a nonlinear differential equation model to explore the dynamics of relapse phenomena and contact differences across health statuses. Our incidence rate function is formulated, taking inspiration from recent adaptive algorithms. It incorporates contact behavior for individuals in each health class. We use constant contact rates at each health status for our analytical results and prove conditions for different forward-backward bifurcation scenarios. The relationship between the different contact rates heavily influences these conditions. Numerical examples highlight the effect of temporarily recovered individuals and initial conditions on infected population persistence.

Keywords: 2000 MSC; 37N25; 92B05; Adaptive behavior; Backward bifurcation; MaMthematical model; Nonlinear incidence; Nonlinear relapse.

Fig. 1

Equilibria points computed using θ = 1.7 and varying κ = 0.8, 0.5, 0.3 and 0.01. A cubic bifurcation plot can be found, and three equilibria points occur within an interval R₀ ∈ [1, 1 + ε(κ, θ)]. We note that decreasing the value of κ diminishes the window ε(κ, θ), and it decreases the minimal R₀ value for which we find stable equilibria, for example, for κ = 0.8 this value is at R₀ ≈ 0.85, but for κ = 0.01 it is at R₀ ≈ 0.8. For a discussion on the length of the window ε(κ, θ), refer to Fig. 5 below. Stable and unstable equilibria regions are highlighted in these plots.

Fig. 2

Equilibria points computed using θ = 1.2 and we varying κ = 0.8, 0.5, 0.3 and 0. We can see that no R₀ allows us to obtain three possible equilibria points.

Fig. 3

Convergence of i(t) to the equilibrium point i∗. On the left, the bifurcation plot was obtained for this case, with region ${\mathcal{R}}_3$ highlighted. The center plot shows cases of convergence to the maximum possible equilibrium point within this region. This happens when the initially infected proportion is high enough. The plot on the right shows cases of convergence towards the smallest equilibrium point in this region, obtained for sufficiently small values of i(0).

Fig. 4

Effect of (κ, θ) for two different initial condition scenarios. On the left using i(0) = 0.1, on the right i(0) = 0.02. For low initial infected populations, a high value of θ yields disease eradication, independently of κ.

Fig. 5

Effect of (κ, θ) on the ${\mathcal{R}}_3$ window length. When θ increases, there is more room to observe this region with more unstable behavior.

Fig. 6

Different infected results varying both contact proportions κ and θ. We keep θ = 1 on the left and vary the proportion κ. Conversely, we keep κ = 1 on the right and vary the value of θ. We observe a bigger effect on the peak prevalence obtained in the figure on the right, that is, varying θ.

Fig. 7

Disease peak infected prevalence varying both contact proportions κ and θ for the influenza simulation example.