SkyPole-A method for locating the north celestial pole from skylight polarization patterns

Abstract

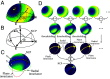
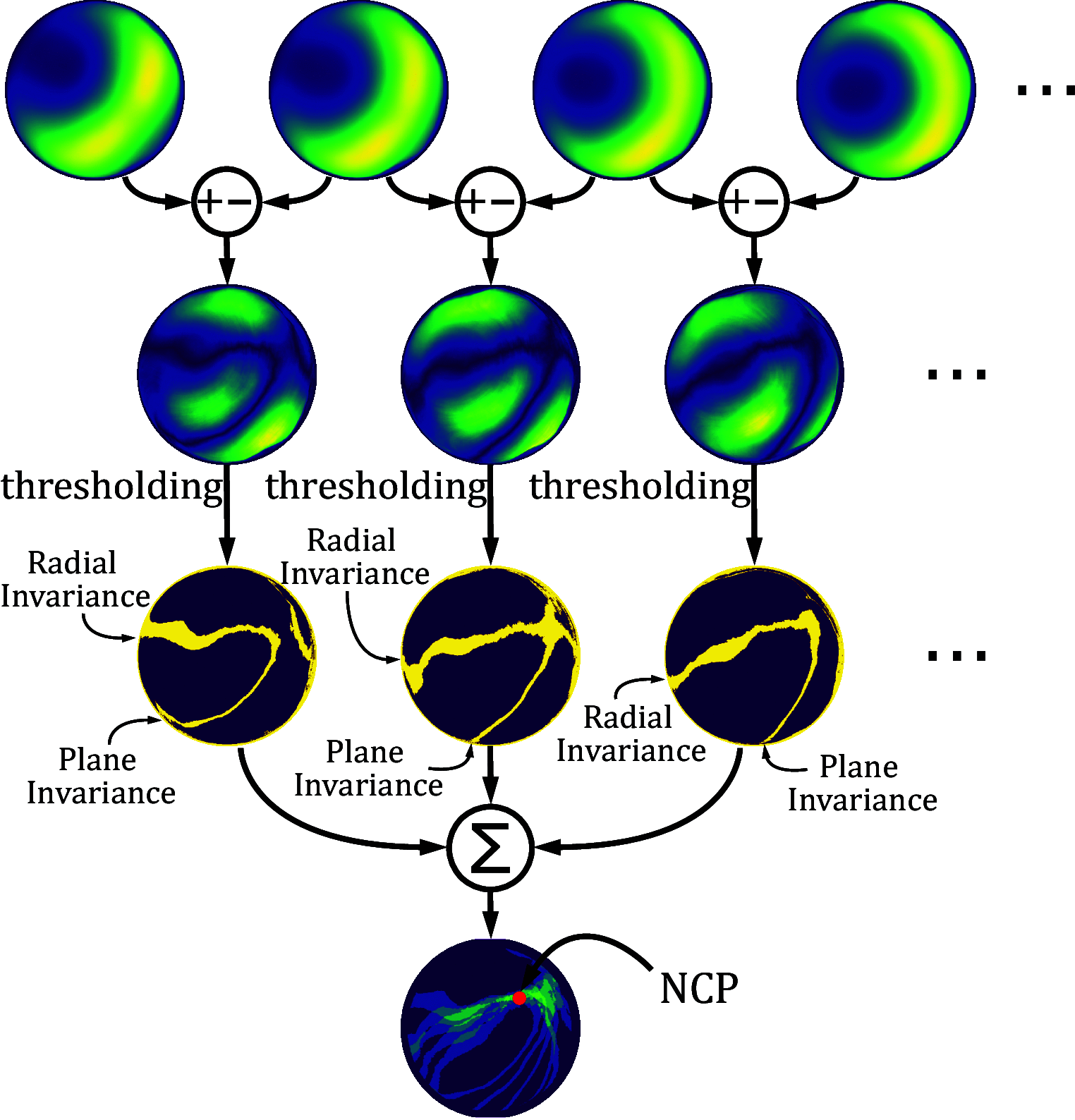
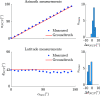
True north can be determined on Earth by three means: magnetic compasses, stars, and via the global navigation satellite systems (GNSS), each of which has its own drawbacks. GNSS are sensitive to jamming and spoofing, magnetic compasses are vulnerable to magnetic interferences, and the stars can be used only at night with a clear sky. As an alternative to these methods, nature-inspired navigational cues are of particular interest. Celestial polarization, which is used by insects such as Cataglyphis ants, can provide useful directional cues. Migrating birds calibrate their magnetic compasses by observing the celestial rotation at night. By combining these cues, we have developed a bioinspired optical method for finding the celestial pole during the daytime. This method, which we have named SkyPole, is based on the rotation of the skylight polarization pattern. A polarimetric camera was used to measure the degree of skylight polarization rotating with the Sun. Image difference processes were then applied to the time-varying measurements in order to determine the north celestial pole's position and thus the observer's latitude and bearing with respect to the true north.

Keywords: GPS-denied environment; celestial compass; celestial navigation; geolocation; polarized vision.

Fig. 1.

(A) Scattering angle γ, azimuth α_P of a point P, and altitude θ_S of the Sun S. Parameters are presented in the ENU frame, namely East, North, and Up frame, centered on the observer O. The colored patterns stand for the skylight DoLP as described in Eq. 1. Dark blue corresponds to near-zero DoLP and yellow to maximum DoLP values (1 in theory, less in reality). (B) The trajectory of the Sun in the ENU frame, centered on an observer O located at latitude ϕ. NCP is the north celestial pole. The Sun moves on a plane perpendicular to the observer–NCP vector. (C) Invariance axis on the celestial sphere. Comparison between simulated and analytical sets of solutions. The green circle is the radial invariance circle; the red circle is the plane invariance circle computed from analytical calculations (cf. SI Appendix). The colored half sphere is the simulated absolute difference between two DoLP patterns associated with the Sun’s positions S₁ and S₂ at two different times. Dark blue corresponds to near-zero values. The red dot is the NCP. (D) Method for finding the NCP based on the skylight’s DoLP pattern. In the first row are the DoLP patterns taken at four different times. Absolute differences between DoLP patterns were then computed, giving the second row. A thresholding step was then applied to those images, and the results are presented in the third row. Last, binary images were summed, and the NCP was then located at the intersection between the radial invariances.

Fig. 2.

SkyPole algorithm applied to experimental data for finding the NCP. Preprocessing of the first row of DoLP images consisted in filtering the images obtained using a circular averaging filter. Details of the following steps are presented in Fig. 1D.

Fig. 3.

NCP coordinates computed with the SkyPole algorithm (Fig. 2) from experimental data versus ground truth NCP coordinates. α_cam is the azimuth of the camera with respect to the north. α_NCP is the azimuth of the NCP with respect to the azimuth of the camera. θ_NCP is the altitude of the NCP, which is also equal to the camera’s latitude. Δα_NCP and Δθ_NCP are the azimuth and altitude error, respectively, of the NCP measured with respect to the ground truth values. n_meas is the number of measurements for each error interval.