Exploring the criticality hypothesis using programmable swarm robots with Vicsek-like interactions

Abstract

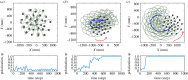
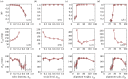
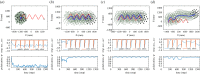
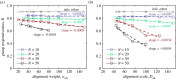
A widely mentioned but not experimentally confirmed view (known as the 'criticality hypothesis') argues that biological swarm systems gain optimal responsiveness to perturbations and information processing capabilities by operating near the critical state where an ordered-to-disordered state transition occurs. However, various factors can induce the ordered-disordered transition, and the explicit relationship between these factors and the criticality is still unclear. Here, we present an experimental validation for the criticality hypothesis by employing real programmable swarm-robotic systems (up to 50 robots) governed by Vicsek-like interactions, subject to time-varying stimulus-response and hazard avoidance. We find that (i) not all ordered-disordered motion transitions correspond to the functional advantages for groups; (ii) collective response of groups is maximized near the critical state induced by alignment weight or scale rather than noise and other non-alignment factors; and (iii) those non-alignment factors act to highlight the functional advantages of alignment-induced criticality. These results suggest that the adjustability of velocity or directional coupling between individuals plays an essential role in the acquisition of maximizing collective response by criticality. Our results contribute to understanding the adjustment strategies of animal interactions from a perspective of criticality and provide insights into the design and control of swarm robotics.

Keywords: alignment; collective response; criticality; ordered–disordered motion transition; self-organization; swarm robots.

Figure 1.

The swarm-robotic system and experimental set-up. (a) The SwarmBang robots. The informed robot with a camera can perceive ambient stimuli, whereas the other uninformed robots are unaware of the stimuli. (b) The experiment arena uses motion capture system to track robots’ position and heading, and a top-view CCD camera to record the trial video. (c) Illustration of the external stimuli. For the attractive stimuli, two different coloured LED lights are installed at the arena edge to attract the informed robot. They alternately light up in a 200-step cycle, guiding the informed robot to perform ${120}^{\circ }$ abrupt turning actions consecutively. For the repulsive stimuli, a faster-moving robot is introduced as a predator to attack the swarm robots.

Figure 2.

Three typical trials of spontaneous collective motion in swarm-robotic experiments. (a) Disordered collective motion with weak alignment weight (w_ali = 15). (b) Ordered collective motion close to the critical state (w_ali = 30). (c) Ordered collective motion with strong alignment weight (w_ali = 100). The thick blue line indicates the trajectory of robotic swarm’s centre. See electronic supplementary material, video S1, for more details.

Figure 3.

Experimental results on spontaneous collective motion. (a) Noise intensity η_m, (b) social level α_soc, (c) alignment weight w_ali, (d) alignment scale D_ali. (a1,b1,c1,d1) The group polarization 〈ψ〉, (a2,b2,c2,d2) the flocking elapsed time T_ord and (a3,b3,c3,d3) the minimum nearest neighbour distance 〈d_nn〉 as a function of these factors, respectively. 〈·〉 symbolizes the average over time; 〈ψ〉 and 〈d_nn〉 are averaged over the last 50 and 200 steps, respectively. The corresponding time-evolving curves of ψ(t) and d_nn(t) are presented in electronic supplementary material, figure S2.

Figure 4.

Four typical trials of collective response in swarm-robotic experiments. (a) Disordered collective motion with weak alignment weight (w_ali = 10, α_soc = 0.5) fails to respond to stimuli. (b) Ordered collective motion close to the critical state (w_ali = 20, α_soc = 0.5) responds rapidly and accurately to stimuli. (c) Ordered collective motion with strong alignment weight (w_ali = 150, α_soc = 0.5) responds inaccurately to stimuli. (d) Ordered collective motion with strong alignment weight and weak social level (w_ali = 150, α_soc = 0.2) fails to respond to stimuli. See electronic supplementary material, video S2, for details.

Figure 5.

Experimental results on collective response to local attractive stimuli. (a) Alignment weight w_ali, (b) alignment scale D_ali, (c) noise intensity η_m, (d) social level α_soc. (a1,b1,c1,d1) The group responsiveness R, (a2,b2,c2,d2) the turning elapsed time T_turn and (a3,b3,c3,d3) the minimum nearest neighbour distance 〈d_nn〉 as a function of these factors, respectively. 〈d_nn〉 is the average of d_nn(t) over time. The corresponding time-evolving curves of acc(t), ψ(t) and d_nn(t) are presented in electronic supplementary material, figure S3.

Figure 6.

Group responsiveness R as a function of alignment weight w_ali and D_ali for different values of (a) noise intensity (η_m = [0, 0.1, 0.15, 0.2]), (b) social level (α_soc = [1, 0.5, 0.3]) and (c) action cycle (τ = [0.2,0.3,0.5]). The dashed lines are fits to a linear dependence of w_ali (D_ali) and R, and their slopes are labelled adjacent to the lines. Note that the data of disordered collective motion are not plotted. The corresponding results of T_turn are presented in electronic supplementary material, figure S4.

Figure 7.

Group responsiveness R as a function of (a) alignment weight w_ali and (b) alignment scale D_ali for different numbers of robots (N = [10, 20, 30, 50]) with α_soc = 0.5. The corresponding results of T_turn are presented in electronic supplementary material, figure S5. Note that the data of disordered collective motion are not plotted.

Figure 8.

Experimental results on collective evasion. (a) D_esp = 30 mm for uninformed robots; (b) D_esp = 300 mm for uninformed robots. (a1,b1) The first capture time T_fc, (a2,b2) the group polarization 〈ψ〉 and (a3,b3) the minimum distance of nearest neighbour 〈d_nn〉 as a function of alignment weight w_ali. 〈ψ〉 and 〈d_nn〉 are averaged over the first 100 steps and all steps after the attacker was detected, respectively. Initially, robotic swarms are placed face-to-face with the attacker, and the informed robot is located at the very front of the group. In these violin plots, each tiny dot represents a trial data, and the big white point represents the median value of the repeated trials.

Figure 9.

Three typical trials of collective evasion in swarm-robotic experiments. (a) The disordered collective motion with weak alignment weight (w_ali = 15); (b) the ordered collective motion close to the critical state (w_ali = 30); (c) the ordered collective motion with strong alignment weight (w_ali = 150). Three rows present robots’ trajectory, profiles of cosine of headings and profiles of polarization, respectively. The grey dashed line indicates the time when the informed robot first detects the attacker. The corresponding snapshots are presented in electronic supplementary material, figure S6; see also video S3 for more information.