Extreme dynamics in a biomolecular condensate
- PMID: 37468629
- PMCID: PMC11508043
- DOI: 10.1038/s41586-023-06329-5
Extreme dynamics in a biomolecular condensate
Abstract
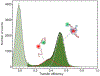
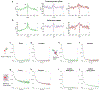
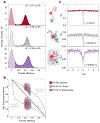
Proteins and nucleic acids can phase-separate in the cell to form concentrated biomolecular condensates1-4. The functions of condensates span many length scales: they modulate interactions and chemical reactions at the molecular scale5, organize biochemical processes at the mesoscale6 and compartmentalize cells4. Understanding the underlying mechanisms of these processes will require detailed knowledge of the rich dynamics across these scales7. The mesoscopic dynamics of biomolecular condensates have been extensively characterized8, but their behaviour at the molecular scale has remained more elusive. Here, as an example of biomolecular phase separation, we study complex coacervates of two highly and oppositely charged disordered human proteins9. Their dense phase is 1,000 times more concentrated than the dilute phase, and the resulting percolated interaction network10 leads to a bulk viscosity 300 times greater than that of water. However, single-molecule spectroscopy optimized for measurements within individual droplets reveals that at the molecular scale, the disordered proteins remain exceedingly dynamic, with their chain configurations interconverting on submicrosecond timescales. Massive all-atom molecular dynamics simulations reproduce the experimental observations and explain this apparent discrepancy: the underlying interactions between individual charged side chains are short-lived and exchange on a pico- to nanosecond timescale. Our results indicate that, despite the high macroscopic viscosity of phase-separated systems, local biomolecular rearrangements required for efficient reactions at the molecular scale can remain rapid.
© 2023. The Author(s), under exclusive licence to Springer Nature Limited.
Conflict of interest statement
Competing interests
The authors declare no competing interests.
Figures


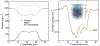




Similar articles
-
Material properties of biomolecular condensates emerge from nanoscale dynamics.Proc Natl Acad Sci U S A. 2025 Jun 10;122(23):e2424135122. doi: 10.1073/pnas.2424135122. Epub 2025 Jun 2. Proc Natl Acad Sci U S A. 2025. PMID: 40455990 Free PMC article.
-
Hydrogen-Bonded Network of Water in Phase-Separated Biomolecular Condensates.J Phys Chem Lett. 2024 Aug 1;15(30):7724-7734. doi: 10.1021/acs.jpclett.4c01153. Epub 2024 Jul 23. J Phys Chem Lett. 2024. PMID: 39042834
-
Heterogeneous Slowdown of Dynamics in the Condensate of an Intrinsically Disordered Protein.J Phys Chem Lett. 2024 Nov 14;15(45):11244-11251. doi: 10.1021/acs.jpclett.4c02142. Epub 2024 Nov 1. J Phys Chem Lett. 2024. PMID: 39486437 Free PMC article.
-
Conformational Dynamics of Intrinsically Disordered Proteins Regulate Biomolecular Condensate Chemistry.Chem Rev. 2022 Mar 23;122(6):6719-6748. doi: 10.1021/acs.chemrev.1c00774. Epub 2022 Feb 18. Chem Rev. 2022. PMID: 35179885 Free PMC article. Review.
-
Recent advances in engineering synthetic biomolecular condensates.Biotechnol Adv. 2024 Dec;77:108452. doi: 10.1016/j.biotechadv.2024.108452. Epub 2024 Sep 11. Biotechnol Adv. 2024. PMID: 39271032 Review.
Cited by
-
BNP-Track: a framework for superresolved tracking.Nat Methods. 2024 Sep;21(9):1716-1724. doi: 10.1038/s41592-024-02349-9. Epub 2024 Jul 22. Nat Methods. 2024. PMID: 39039336 Free PMC article.
-
Biomolecular condensates form spatially inhomogeneous network fluids.Nat Commun. 2024 Apr 22;15(1):3413. doi: 10.1038/s41467-024-47602-z. Nat Commun. 2024. PMID: 38649740 Free PMC article.
-
Molecular insights into the interaction between a disordered protein and a folded RNA.bioRxiv [Preprint]. 2024 Jun 12:2024.06.12.598678. doi: 10.1101/2024.06.12.598678. bioRxiv. 2024. Update in: Proc Natl Acad Sci U S A. 2024 Dec 3;121(49):e2409139121. doi: 10.1073/pnas.2409139121. PMID: 38915483 Free PMC article. Updated. Preprint.
-
Recent Progress in Modeling and Simulation of Biomolecular Crowding and Condensation Inside Cells.J Chem Inf Model. 2024 Dec 23;64(24):9063-9081. doi: 10.1021/acs.jcim.4c01520. Epub 2024 Dec 11. J Chem Inf Model. 2024. PMID: 39660892 Free PMC article. Review.
-
Dynamical control enables the formation of demixed biomolecular condensates.Nat Commun. 2023 Nov 24;14(1):7678. doi: 10.1038/s41467-023-43489-4. Nat Commun. 2023. PMID: 37996438 Free PMC article.
References
-
- Abascal JLF, and Vega C. 2005. ‘A general purpose model for the condensed phases of water: TIP4P/2005’, J. Chem. Phys, 123: 234505. - PubMed
-
- Abraham MJ, Murtola T, Schulz R, Pall S, Smith JC, Hess B, and Lindahl E. 2015. ‘GROMACS: High performance molecular simulations through multi-levelvparallelism from laptops to supercomputers’, SoftwareX, 1-2: 19–25.
-
- Alberts Bruce. 2022. Molecular biology of the cell (W. W. Norton & Company: New York: ).
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

