Dense Disordered Jammed Packings of Hard Spherocylinders with a Low Aspect Ratio: A Characterization of Their Structure

Abstract

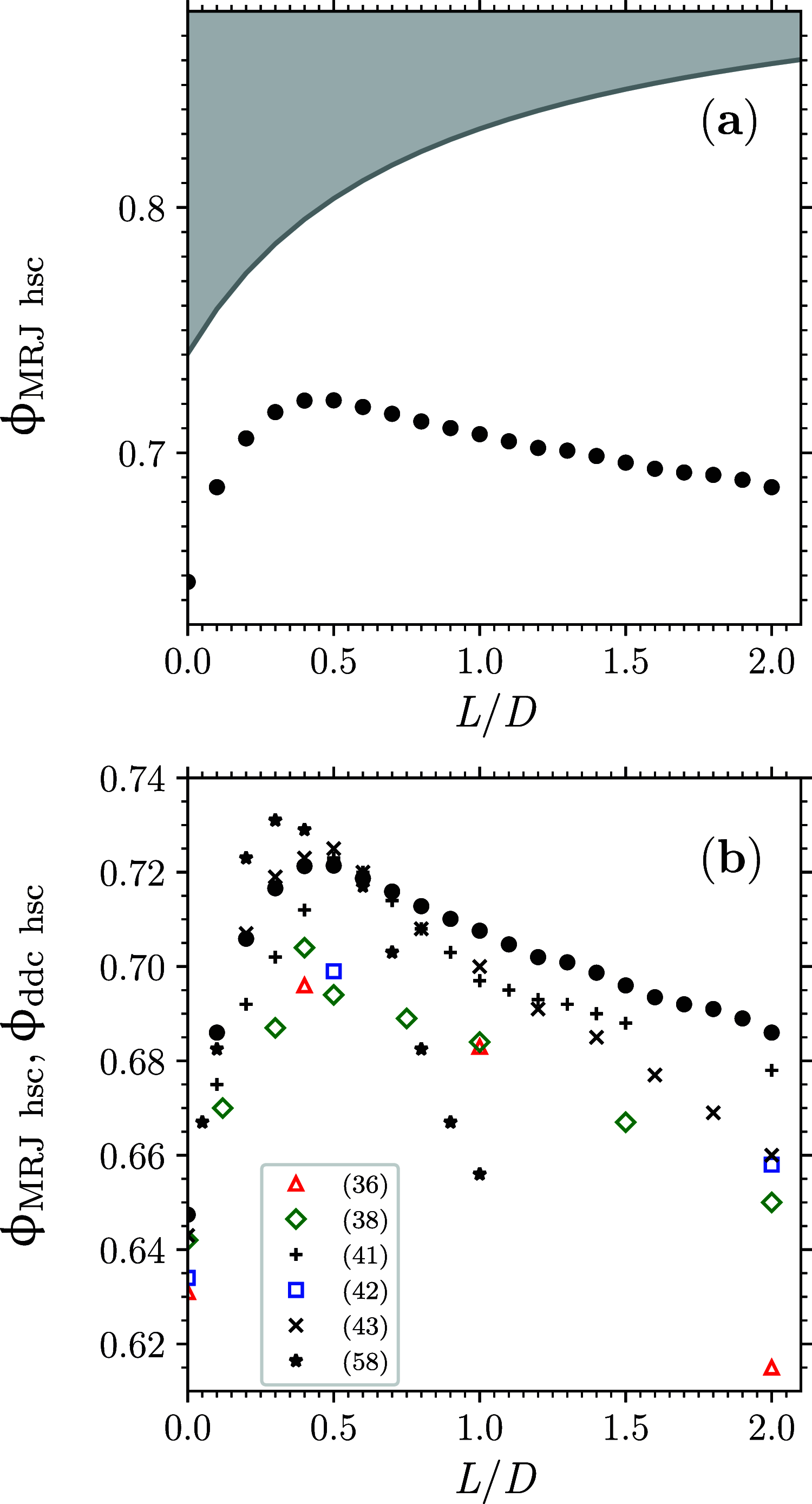
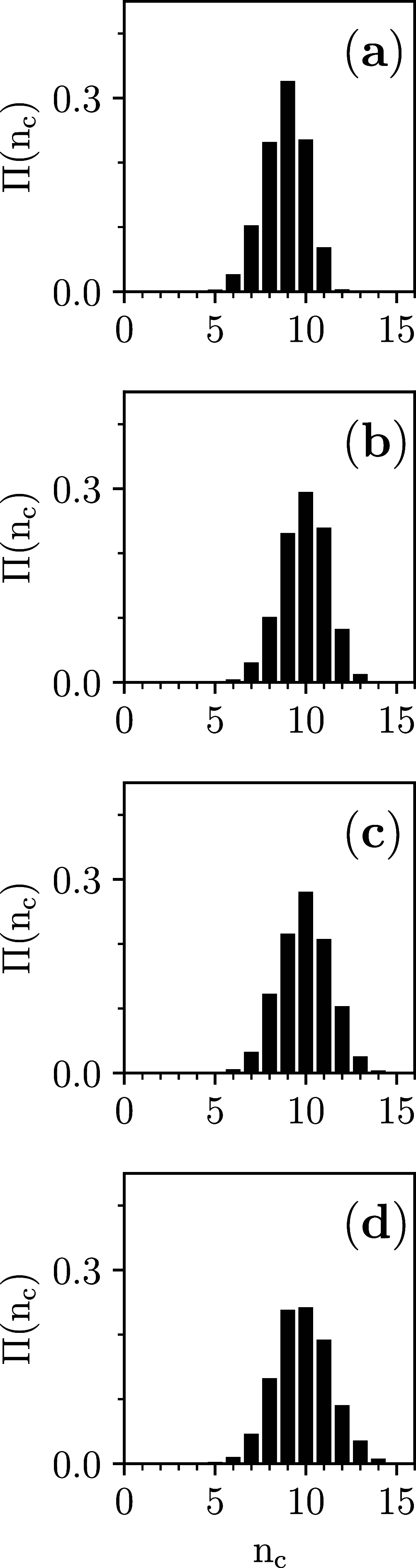
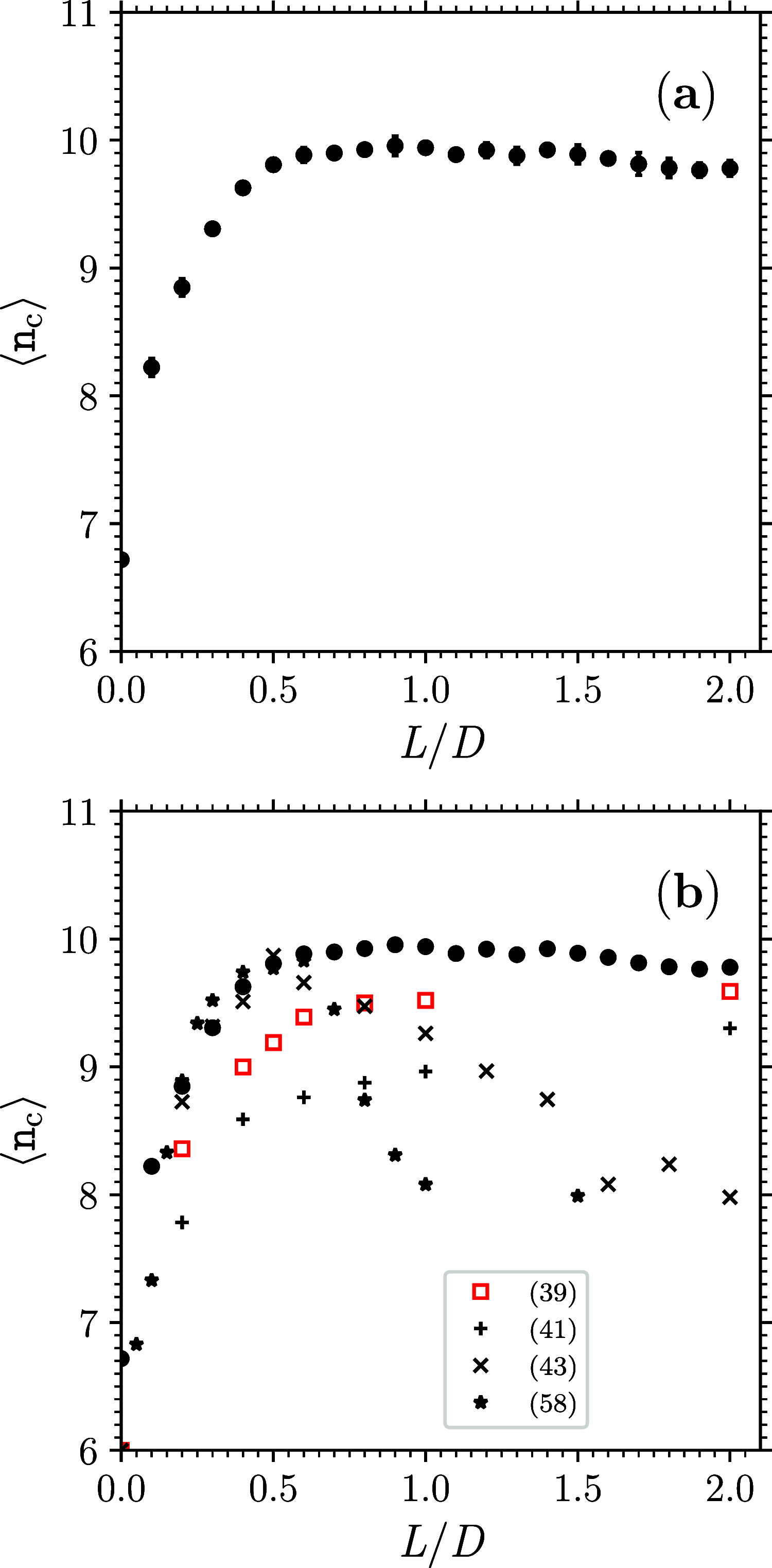
This work numerically investigates dense disordered (maximally random) jammed packings of hard spherocylinders of cylinder length L and diameter D by focusing on L/D ∈ [0,2]. It is within this interval that one expects that the packing fraction of these dense disordered jammed packings ϕ_{MRJ hsc} attains a maximum. This work confirms the form of the graph ϕ_{MRJ hsc} versus L/D: here, comparably to certain previous investigations, it is found that the maximal ϕ_{MRJ hsc} = 0.721 ± 0.001 occurs at L/D = 0.45 ± 0.05. Furthermore, this work meticulously characterizes the structure of these dense disordered jammed packings via the special pair-correlation function of the interparticle distance scaled by the contact distance and the ensuing analysis of the statistics of the hard spherocylinders in contact: here, distinctly from all previous investigations, it is found that the dense disordered jammed packings of hard spherocylinders with 0.45 ≲ L/D ≤ 2 are isostatic.

Figure 1

Example spherocylinder, specifically one with L/D = 2, with L as the length of the central cylindrical part and D as the diameter of the central cylindrical part and of the two extremal hemispherical parts. The image was produced by the program QMGA.

Figure 2

(a) Maximally random jammed state packing fraction of hard spherocylinders ϕ_MRJ hsc as a function of L/D (black circles; data are the average over the respective seven jammed configurations; the error bars, which typically are ∼0.001, are the corresponding standard deviation; the gray region corresponds to those values of ϕ that are prohibited as they are larger than the corresponding value of ϕ_max hsc). (b) Comparison of the present data of ϕ_MRJ hsc (black circles) with previous data of ϕ of dense disordered compact packings of hard spherocylinders ϕ_ddc hsc (various symbols, each symbol corresponding to a previous work as the legend indicates).

Figure 3

Example image of a jammed configuration of hard spherocylinders with L/D = 0.5. The color or tint of gray of a hard spherocylinder is related to the angle that its cylindrical axis forms with an arbitrary axis, e.g., the y-axis, of the frame of reference. The image was produced by the program QMGA.

Figure 4

Pair-correlation functions g(r), G₂^û(r), and G₂^r̂(r) for dense disordered jammed packings of hard spherocylinders with (a, b, c) L/D = 0.3; (d, e, f) L/D = 1.1; and (g, h, i) L/D = 1.9 (in each panel, the graph is the average over the respective seven jammed configurations).

Figure 5

Pair-correlation function g(s) for dense disordered jammed packings of hard spherocylinders with (a) L/D = 0; (b) L/D = 0.5; (c) L/D = 1; and (d) L/D = 1.5 (in each panel, the graph is the average over the respective seven jammed configurations). In panel (a), the present g(s) (black) is compared with the accurate hard-sphere MRJ g(r/D) (red or gray) that was previously calculated.

Figure 6

Probability distribution of the number of contacts per hard spherocylinder Π(n_c) for dense disordered jammed packings of hard spherocylinders with (a) L/D = 0.2; (b) L/D = 0.7; (c) L/D = 1.2; and (d) L/D = 1.7 (in each panel, the histogram is the average over the respective seven jammed configurations).

Figure 7

(a) Mean number of contacts per hard spherocylinder ⟨n_c⟩ as a function of L/D (black circles; data are the average over the respective seven jammed configurations; the error bars, which typically are ∼0.05, are the corresponding standard deviation). (b) Comparison of the present data of ⟨n_c⟩ (black circles) with previous data of ⟨n_c⟩ of dense disordered compact packings of hard spherocylinders (various symbols, each symbol corresponding to a previous work as the legend indicates).

Figure 8

(a) Fractions of cylinder–cylinder contacts f_cc, cylinder–sphere contacts f_cs, and sphere–sphere contacts f_ss as a function of L/D (black empty symbols; data are the average over the respective seven jammed configurations; the error bars, which typically are ∼0.01, are the corresponding standard deviation). (One observes that f_cc and f_cs do not seem to extrapolate to zero nor f_ss to unity as L/D → 0.) (b) Comparison of the present data of f_cc, f_cs, and f_ss (black empty symbols) with previous data of f_cc, f_cs, and f_ss of dense disordered compact packings of hard spherocylinders (red or darker gray and yellow or lighter gray filled symbols, each symbol corresponding to a previous work as the legend indicates).

Figure 9

Pair-correlation function g_cp(r) for dense disordered jammed packings of hard spherocylinders with (a) L/D = 0; (b) L/D = 0.5; (c) L/D = 1; and (d) L/D = 1.5 (in each panel, the graph is the average over the respective seven jammed configurations). In panel (a), the present g_cp(r) corresponds to the hard-sphere “contacts RDF” that was previously calculated.