Sequential Attractors in Combinatorial Threshold-Linear Networks
- PMID: 37485069
- PMCID: PMC10362966
- DOI: 10.1137/21m1445120
Sequential Attractors in Combinatorial Threshold-Linear Networks
Abstract
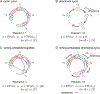
Sequences of neural activity arise in many brain areas, including cortex, hippocampus, and central pattern generator circuits that underlie rhythmic behaviors like locomotion. While network architectures supporting sequence generation vary considerably, a common feature is an abundance of inhibition. In this work, we focus on architectures that support sequential activity in recurrently connected networks with inhibition-dominated dynamics. Specifically, we study emergent sequences in a special family of threshold-linear networks, called combinatorial threshold-linear networks (CTLNs), whose connectivity matrices are defined from directed graphs. Such networks naturally give rise to an abundance of sequences whose dynamics are tightly connected to the underlying graph. We find that architectures based on generalizations of cycle graphs produce limit cycle attractors that can be activated to generate transient or persistent (repeating) sequences. Each architecture type gives rise to an infinite family of graphs that can be built from arbitrary component subgraphs. Moreover, we prove a number of graph rules for the corresponding CTLNs in each family. The graph rules allow us to strongly constrain, and in some cases fully determine, the fixed points of the network in terms of the fixed points of the component subnetworks. Finally, we also show how the structure of certain architectures gives insight into the sequential dynamics of the corresponding attractor.
Keywords: 34A34; 92C20; attractor dynamics; network architectures; neuronal sequences; threshold-linear networks.
Figures
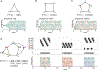



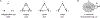
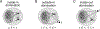


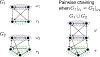
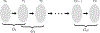





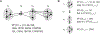

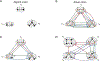

References
-
- Abeles M, Local Cortical Circuits: An Electrophysiological Study, Springer, Berlin, 1982.
-
- Aviel Y, Pavlov E, Abeles M, and Horn D, Synfire chain in a balanced network, Neurocomput., 44 (2002), pp. 285–292.
-
- Bel A, Cobiaga R, Reartes W, and Rotstein HG, Periodic solutions in threshold-linear networks and their entrainment, SIAM J. Appl. Dyn. Syst, 20 (2021), pp. 1177–1208.
-
- Biswas T and Fitzgerald JE, A Geometric Framework to Predict Structure from Function in Neural networks, https://arxiv.org/abs/2010.09660, 2022. - PMC - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
