MODELING CELL POPULATIONS MEASURED BY FLOW CYTOMETRY WITH COVARIATES USING SPARSE MIXTURE OF REGRESSIONS
- PMID: 37485300
- PMCID: PMC10360992
- DOI: 10.1214/22-aoas1631
MODELING CELL POPULATIONS MEASURED BY FLOW CYTOMETRY WITH COVARIATES USING SPARSE MIXTURE OF REGRESSIONS
Abstract
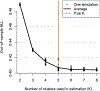
The ocean is filled with microscopic microalgae, called phytoplankton, which together are responsible for as much photosynthesis as all plants on land combined. Our ability to predict their response to the warming ocean relies on understanding how the dynamics of phytoplankton populations is influenced by changes in environmental conditions. One powerful technique to study the dynamics of phytoplankton is flow cytometry which measures the optical properties of thousands of individual cells per second. Today, oceanographers are able to collect flow cytometry data in real time onboard a moving ship, providing them with fine-scale resolution of the distribution of phytoplankton across thousands of kilometers. One of the current challenges is to understand how these small- and large-scale variations relate to environmental conditions, such as nutrient availability, temperature, light and ocean currents. In this paper we propose a novel sparse mixture of multivariate regressions model to estimate the time-varying phytoplankton subpopulations while simultaneously identifying the specific environmental covariates that are predictive of the observed changes to these subpopulations. We demonstrate the usefulness and interpretability of the approach using both synthetic data and real observations collected on an oceanographic cruise conducted in the northeast Pacific in the spring of 2017.
Keywords: Mixture of regressions; alternating direction method of multipliers; clustering; expectation-maximization; flow cytometry; gating; microbiome; ocean; phytoplankton; sparse regression.
Figures

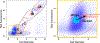

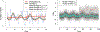
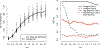

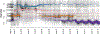

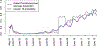
References
-
- Ashkezari MD, Hagen NR, Denholtz M, Neang A, Burns TC, Morales RL, Lee CP, Hill CN and Armbrust EV (2021). Simons collaborative marine atlas project (Simons CMAP): An open-source portal to share, visualize and analyze ocean data. BioRxiv
-
- Boyd S, Parikh N, Chu E, Peleato B and Eckstein J (2011). Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn 3 1–122.
-
- Boyer TP, Antonov JI, Baranova OK, Garcia HE, Johnson DR, Mishonov AV, O’Brien TD, Seidov D, Smolyar II et al. (2013). World ocean database 2013
