Network bypasses sustain complexity

Abstract

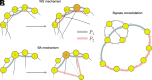
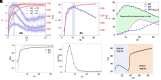
Real-world networks are neither regular nor random, a fact elegantly explained by mechanisms such as the Watts-Strogatz or the Barabási-Albert models, among others. Both mechanisms naturally create shortcuts and hubs, which while enhancing the network's connectivity, also might yield several undesired navigational effects: They tend to be overused during geodesic navigational processes-making the networks fragile-and provide suboptimal routes for diffusive-like navigation. Why, then, networks with complex topologies are ubiquitous? Here, we unveil that these models also entropically generate network bypasses: alternative routes to shortest paths which are topologically longer but easier to navigate. We develop a mathematical theory that elucidates the emergence and consolidation of network bypasses and measure their navigability gain. We apply our theory to a wide range of real-world networks and find that they sustain complexity by different amounts of network bypasses. At the top of this complexity ranking we found the human brain, which points out the importance of these results to understand the plasticity of complex systems.

Keywords: communicability paths; complex networks; geometric embedding.

Fig. 1.

(A) Illustration of the effects of the edge rewiring process in the Watts–Strogatz model on the paths connecting two arbitrary vertices of the resulting graph: the shortest path $P_1$ (blue) can be bypassed by the path $P_2$ (pink), topologically longer but with a lower energetic cost. (B) A similar phenomenon happens when the node $h$ becomes a hub after a rich-get-richer mechanism. The shortest path $P_1$ (blue) typically crosses the hub but, with a sufficiently large mean degree, other paths such as $P_2$ (pink) can bypass the shortest path $P_1$, allowing alternative routes when hubs reach capacity and become saturated or damaged. (C) Navigational dilemma embedded in a network: The blue path $P_1$ is the shortest path, but it turns out that the pink “braquistochronic” path $P_2$ is more advantageous as it avoids congestion and is less resistive (see SI Appendix, section S5 for an explicit calculation).

Fig. 2.

Plot of the normalized communicability entropy $\widehat{S}(\mathbf{q})$ (red) and of the net gain factor $ϵ$ (blue) vs. : (A) the rewiring probability $p$ for WS networks (numerical step of $\delta p=0.01$) with $n=250$ nodes and different average degree $⟨k⟩$, or (B) the mean degree $⟨k⟩$ of a BA model with $n=250$ nodes. Each dot is the average of 100 realizations, and standard deviations over the ensemble of realizations are also depicted. In both panels, the shaded blue area highlights the maximum of $ϵ$ and marks the network’s good navigational point $(p_{\text{GNP}}\approx 0.15$ for WS model, ${⟨k⟩}_{\text{GNP}}\approx 11$ for BA model). (C) $ϵ$ vs $⟨k⟩$ for networks of $n=250$ nodes generated via the BA model, the WS model (poised at the good navigational point), and an Erdos-Renyi (ER) model for comparison. The bypass-induced navigability gain is substantially larger in heterogeneous (BA) networks than in more homogeneous ones. The comparison between ER and SW networks is nontrivial and can be explained in terms of the shapes of the respective degree distributions as $⟨k⟩$ increases (see the text and SI Appendix). (D) Normalized communicability entropy of both BA and ER networks with the same number of nodes, as a function of the mean degree. (E) Ratio ${ϵ}_{\text{BA}}/{ϵ}_{\text{ER}}$ to highlight the difference in navigability gains displayed in panel (C). (F) ${ϵ}_{\mathit{BA}}$ vs $⟨k⟩$ in the extended region of high density, where preferential attachment is not properly working anymore (SI Appendix, S9), leading to an explosion of the navigability gain due to the transition to ultrashort graphs.

Fig. 3.

(A) Toy network with a concrete source–destination pair $(p,q)$, which can be navigated via paths $P_1$ and $P_2$. (B) Computation of the different metrics certifies that $P_2$ is a bypass of the shortest path $P_1$, and the navigability gain associated with this pair is $25\%$ (a lower bound of the actual gain; see SI Appendix, S5). Random walk trajectories starting at $p$ and eventually hitting $q$ can be classified as $P_1$-like or $P_2$-like, depending on their specific trajectories (SI Appendix, S6). The hitting time and excess time of the $P_1$ class is larger than for $P_2$, meaning that random-walk navigability is enhanced in the $P_2$ (that is, the SRP) class. The excess time saving is a diffusion-proxy of the navigability gain (SI Appendix, S6). (C) Coactivation brain network. (D) Excess time saving for several source–destination pairs in the brain network, finding that SRP enhances navigability in all cases.

Fig. 4.

Some scatter plots of the metrics reported in Table 1 for empirical networks. (Left) Net navigability gain $ϵ$ vs $p^{\ast }$, revealing the emergence of two well-defined groups of networks. (Centre) Navigability ratio $ϵ/{ϵ}_{\text{BA}}$ vs. $p^{\ast }$, finding the same clustering as in panel (left). (Right) $ϵ$ vs. the normalized communicability entropy $\widehat{S}(\mathbf{q})$, where no clear clustering emerges.